question_answer

Two point light sources are 24 cm apart. Where should a convex lens of focal length 9 cm be put in between them from one source so that the images of both the sources are formed at the same place

A) 6 cm

B) 9 cm

C) 12 cm

D) 15 cm

Correct Answer: A

Solution :

[a] The given condition will be satisfied only if one source \[({{S}_{1}})\] placed on one side such that \[u<f\] (i.e., it lies under the focus). The other source (5y is placed on the other side of the lens such that \[u>f\] (i.e., it lies beyond the focus).

If \[{{S}_{1}}\] is the object for lens, then
\[\frac{1}{f}=\frac{1}{-y}-\frac{1}{-x}\,\,\Rightarrow \,\,\frac{1}{y}=\frac{1}{x}-\frac{1}{f}\]	....(i)

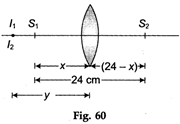If \[{{S}_{2}}\] is the object for lens, then
\[\frac{1}{f}=\frac{1}{+y}\,-\frac{1}{-(24-x)}\]
\[\Rightarrow \]            \[\frac{1}{y}=\frac{1}{y}-\frac{1}{(24-x)}\]	...(ii)

From (i) and (ii),

\[\frac{1}{x}-\frac{1}{f}=\frac{1}{f}-\frac{1}{(24-x)}\]

\[\Rightarrow \]   \[\frac{1}{x}+\frac{1}{(24-x)}=\frac{2}{f}=\frac{2}{9}\]

\[\Rightarrow \]   \[{{x}^{2}}-24x+108=0\]

On solving the equation, \[x=18\text{ }cm,\text{ }6\text{ }cm\]