A) 6.67 cm left
B) 6.67 cm right
C) 15.0 cm left
D) 15.0 cm right
Correct Answer: A
Solution :
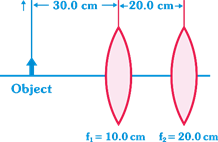
[a] First we make ray diagrams roughly to scale to see where the image from the first lens falls and how it acts as the object for the second lens. The location of the image formed by the first lens is found via the thin-lens equation: \[\frac{1}{30.0}+\frac{1}{{{v}_{1}}}=\frac{1}{10.0}\] \[{{v}_{1}}=+15.0\,cm\]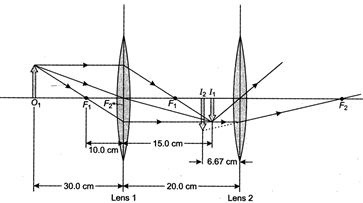 The image formed by this lens becomes the object for the second lens. Thus, the object distance for the second lens is \[20.0\text{ }cm-15.0\text{ }cm=\text{ }5.00\text{ }cm\]. We again apply the thin-lens equation to find the location of the final image \[\frac{1}{5.00}+\frac{1}{{{v}_{2}}}=\frac{1}{20.0}\]\[{{v}_{2}}=-6.67cm\]. Thus, the final image is 6.67 cm to the left of the second lens.
The image formed by this lens becomes the object for the second lens. Thus, the object distance for the second lens is \[20.0\text{ }cm-15.0\text{ }cm=\text{ }5.00\text{ }cm\]. We again apply the thin-lens equation to find the location of the final image \[\frac{1}{5.00}+\frac{1}{{{v}_{2}}}=\frac{1}{20.0}\]\[{{v}_{2}}=-6.67cm\]. Thus, the final image is 6.67 cm to the left of the second lens.
You need to login to perform this action.
You will be redirected in
3 sec
