A) \[3\sqrt{3}:1\]
B) \[\sqrt{3}:4\]
C) \[\sqrt{3}:8\]
D) \[3\sqrt{3}:2\]
Correct Answer: D
Solution :
[d]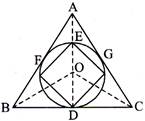 In the given figure ABC is an equilateral \[\Delta \] of a side with a circle inscribed in it and a square inscribed in the circle. AD, BO and CO are the angle bisectors of\[\angle A\], \[\angle B\] and \[\angle c\] and 0 is the centre of the circle. We know that the angle bisector from the vertex of an equilateral triangle is the perpendicular bisector of the opposite side. AD is the perpendicular bisector of BC. \[\Rightarrow \,\,\,BD=\frac{a}{2}\,\,and\,\,\angle DOB=\frac{1}{2}\angle B=\frac{1}{2}\times 60{}^\circ =30{}^\circ \] Now in \[\Delta BOD\] \[\tan 30{}^\circ =\frac{OD}{BD}=\frac{Radius\,of\,circle}{\frac{a}{2}}\] \[\Rightarrow \]Radius of circle\[=\frac{1}{\sqrt{3}}\times \frac{a}{2}=\frac{2}{2\sqrt{3}}\] Now in right \[\Delta EDG\] \[E{{G}^{2}}+G{{D}^{2}}=E{{D}^{2}}\](Pythagoras theorem) \[2\,\,{{(EG)}^{2}}=2\,\,{{(OD)}^{2}}={{\left( \frac{a}{\sqrt{3}} \right)}^{2}}=\frac{{{a}^{2}}}{3}\] Side of the square \[=\sqrt{\frac{{{a}^{2}}}{6}}=\frac{a}{\sqrt{6}}\] Now \[ar\] \[(\Delta ABC):\,\,ar\,\,(\Delta EFG)\] \[\frac{\frac{\sqrt{3}}{4}{{a}^{2}}}{\frac{a}{\sqrt{6}}\times \frac{a}{\sqrt{6}}}=\frac{\frac{\sqrt{3}}{4}}{\frac{1}{6}}=3\sqrt{3}:2\]
In the given figure ABC is an equilateral \[\Delta \] of a side with a circle inscribed in it and a square inscribed in the circle. AD, BO and CO are the angle bisectors of\[\angle A\], \[\angle B\] and \[\angle c\] and 0 is the centre of the circle. We know that the angle bisector from the vertex of an equilateral triangle is the perpendicular bisector of the opposite side. AD is the perpendicular bisector of BC. \[\Rightarrow \,\,\,BD=\frac{a}{2}\,\,and\,\,\angle DOB=\frac{1}{2}\angle B=\frac{1}{2}\times 60{}^\circ =30{}^\circ \] Now in \[\Delta BOD\] \[\tan 30{}^\circ =\frac{OD}{BD}=\frac{Radius\,of\,circle}{\frac{a}{2}}\] \[\Rightarrow \]Radius of circle\[=\frac{1}{\sqrt{3}}\times \frac{a}{2}=\frac{2}{2\sqrt{3}}\] Now in right \[\Delta EDG\] \[E{{G}^{2}}+G{{D}^{2}}=E{{D}^{2}}\](Pythagoras theorem) \[2\,\,{{(EG)}^{2}}=2\,\,{{(OD)}^{2}}={{\left( \frac{a}{\sqrt{3}} \right)}^{2}}=\frac{{{a}^{2}}}{3}\] Side of the square \[=\sqrt{\frac{{{a}^{2}}}{6}}=\frac{a}{\sqrt{6}}\] Now \[ar\] \[(\Delta ABC):\,\,ar\,\,(\Delta EFG)\] \[\frac{\frac{\sqrt{3}}{4}{{a}^{2}}}{\frac{a}{\sqrt{6}}\times \frac{a}{\sqrt{6}}}=\frac{\frac{\sqrt{3}}{4}}{\frac{1}{6}}=3\sqrt{3}:2\]
You need to login to perform this action.
You will be redirected in
3 sec
