question_answer

If\[x\,\,\sin \theta -y\cos \theta =\sqrt{{{x}^{2}}+{{y}^{2}}}\]and\[\frac{{{\cos }^{2}}\theta }{{{a}^{2}}}+\frac{{{\sin }^{2}}\theta }{{{b}^{2}}}=\frac{1}{{{x}^{2}}+{{y}^{2}}},\]then the correct relation is                                [SSC (10+2) 2013]

A) \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\]            

B) \[\frac{{{x}^{2}}}{{{b}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]

C) \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\]              

D) \[\frac{{{x}^{2}}}{{{b}^{2}}}-\frac{{{y}^{2}}}{{{a}^{2}}}=1\]

Correct Answer: B

Solution :

Given, \[x\sin \theta -y\cos \theta =\sqrt{{{x}^{2}}+{{y}^{2}}}\]

On squaring both sides, we get

\[{{(x\sin \theta -y\cos \theta )}^{2}}={{(\sqrt{{{x}^{2}}+{{y}^{2}}})}^{2}}\]

\[\Rightarrow \]\[{{x}^{2}}{{\sin }^{2}}\theta +{{y}^{2}}{{\cos }^{2}}\theta -2xy\]

\[\sin \theta \cos \theta ={{x}^{2}}+{{y}^{2}}\]

\[\Rightarrow \]\[{{x}^{2}}{{\sin }^{2}}\theta +{{y}^{2}}{{\cos }^{2}}\theta \]

\[-\,\,2xy\sin \theta \cos \theta -{{x}^{2}}-{{y}^{2}}=0\]

\[\Rightarrow \]\[{{x}^{2}}{{\sin }^{2}}\theta -{{x}^{2}}+{{y}^{2}}{{\cos }^{2}}\theta -{{y}^{2}}\]

\[-\,\,2xy\sin \theta \cos \theta =0\]

\[\Rightarrow \]\[{{x}^{2}}\,\,({{\sin }^{2}}\theta -1)+{{y}^{2}}\,\,({{\cos }^{2}}\theta -1)\]

\[-\,\,2xy\sin \theta \cos \theta =0\]

\[\Rightarrow \]\[-{{x}^{2}}{{\cos }^{2}}\theta -{{y}^{2}}{{\sin }^{2}}\theta \]

\[-\,\,2xy\sin \theta \cos \theta =0\]

\[\Rightarrow \]\[{{(x\cos \theta +y\,\,\sin \theta )}^{2}}=0\]                                             \[[\because {{a}^{2}}+{{b}^{2}}+2ab={{(a+b)}^{2}}]\]

\[\Rightarrow \]   \[x\cos \theta +y\sin \theta =0\]

\[\Rightarrow \]               \[x\cos \theta =-\,y\sin \theta \]

\[\Rightarrow \]               \[\tan \theta =-\frac{x}{y}\]

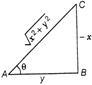In \[\Delta ABC,\]\[\sin \theta =\frac{BC}{AC}\]

\[\Rightarrow \]\[\sin \theta =\frac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\]or \[-\frac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\]

Similarly, \[\cos \theta =-\frac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\]or \[\frac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\]

Now, \[\frac{{{\cos }^{2}}\theta }{{{a}^{2}}}+\frac{{{\sin }^{2}}\theta }{{{b}^{2}}}=\frac{1}{{{x}^{2}}+{{y}^{2}}}\]

\[\Rightarrow \]\[\frac{{{y}^{2}}}{({{x}^{2}}+{{y}^{2}})\cdot {{a}^{2}}}+\frac{{{x}^{2}}}{({{x}^{2}}+{{y}^{2}})\cdot {{b}^{2}}}=\frac{1}{{{x}^{2}}+{{y}^{2}}}\]

\[\Rightarrow \]\[\frac{{{y}^{2}}}{{{a}^{2}}}+\frac{{{x}^{2}}}{{{b}^{2}}}=1\]\[\Rightarrow \]\[\frac{{{x}^{2}}}{{{b}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]