| A galvanometer having 30 division scale and \[100\,\Omega \] resistance is connected in series to the battery of emf 3 V through a resistance of \[200\,\Omega ,\] shows full scale deflection. Find the figure of merit of the galvanometer in microampere. |
| Or |
| A circular segment of radius 10 cm, subtends an angle of \[60{}^\circ \] at its centre. A current of 9 A is flowing through it. Find the magnitude and direction of the magnetic field produced at the centre. |
Answer:
Here, n = 30, \[G=100\,\Omega ,\] E = 3 V, \[R=200\,\Omega ,\] k = ? Total resistance \[=G+R=100+200=300\,\Omega \] \[{{I}_{g}}=\frac{E}{G+R}=\frac{3}{300}=\frac{1}{100}A\] \[k=\frac{{{I}_{g}}}{n}=\frac{1/100}{30}\] or \[k=(1/3)\times {{10}^{-3}}A/division\] or \[k=(1/3)\times {{10}^{-3}}\times {{10}^{6}}\mu A/division\] or \[k=333.3\mu A/division\] Or Given, r = 10 cm = 0.1 m \[\theta =60{}^\circ =\pi /3rad\] I = 9 A, B = ? 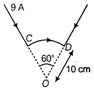 Here, CD is the circular segment with centre O, in the plane of paper. Let l = length of segment CD. It subtends an angle \[60{}^\circ =(\pi /3)\]at 0, i.e. \[\alpha =\pi /3\,rad.\] Now magnetic field induction at O due to current through segment CD will be \[B=\frac{{{\mu }_{0}}l}{4\pi r}\alpha =\frac{{{\mu }_{0}}l}{4\pi r}.\frac{\pi }{3}\] or \[={{10}^{-7}}\times \frac{9}{0.1}\times \frac{3.14}{3}=9.42\times {{10}^{-6}}T\] The direction of magnetic field induction, according to right hand rule will be downwards perpendicular to the plane of paper.
Here, CD is the circular segment with centre O, in the plane of paper. Let l = length of segment CD. It subtends an angle \[60{}^\circ =(\pi /3)\]at 0, i.e. \[\alpha =\pi /3\,rad.\] Now magnetic field induction at O due to current through segment CD will be \[B=\frac{{{\mu }_{0}}l}{4\pi r}\alpha =\frac{{{\mu }_{0}}l}{4\pi r}.\frac{\pi }{3}\] or \[={{10}^{-7}}\times \frac{9}{0.1}\times \frac{3.14}{3}=9.42\times {{10}^{-6}}T\] The direction of magnetic field induction, according to right hand rule will be downwards perpendicular to the plane of paper.
You need to login to perform this action.
You will be redirected in
3 sec
