question_answer

A galvanometer having 30 division scale and \[100\,\Omega \] resistance is connected in series to the battery of emf 3 V through a resistance of \[200\,\Omega ,\] shows full scale deflection. Find the figure of merit of the galvanometer in microampere.

Or

A circular segment of radius 10 cm, subtends an angle of \[60{}^\circ \] at its centre. A current of 9 A is flowing through it. Find the magnitude and direction of the magnetic field produced at the centre.

Answer:

Here, n = 30, \[G=100\,\Omega ,\] E = 3 V, \[R=200\,\Omega ,\] k = ? Total resistance   \[=G+R=100+200=300\,\Omega \]             \[{{I}_{g}}=\frac{E}{G+R}=\frac{3}{300}=\frac{1}{100}A\]             \[k=\frac{{{I}_{g}}}{n}=\frac{1/100}{30}\] or         \[k=(1/3)\times {{10}^{-3}}A/division\] or         \[k=(1/3)\times {{10}^{-3}}\times {{10}^{6}}\mu A/division\] or         \[k=333.3\mu A/division\] Or Given,   r = 10 cm = 0.1 m             \[\theta =60{}^\circ =\pi /3rad\]             I = 9 A, B = ? 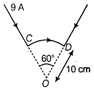Here, CD is the circular segment with centre O, in the plane of paper. Let l = length of segment CD. It subtends an angle \[60{}^\circ =(\pi /3)\]at 0, i.e. \[\alpha =\pi /3\,rad.\] Now magnetic field induction at O due to current through segment CD will be \[B=\frac{{{\mu }_{0}}l}{4\pi r}\alpha =\frac{{{\mu }_{0}}l}{4\pi r}.\frac{\pi }{3}\] or  \[={{10}^{-7}}\times \frac{9}{0.1}\times \frac{3.14}{3}=9.42\times {{10}^{-6}}T\] The direction of magnetic field induction, according to right hand rule will be downwards perpendicular to the plane of paper.