question_answer

Define resistivity of a conductor. How does the resistivity of a metallic conductor changes with temperature? Draw approximate graph of resistivity plotted against temperature for

(i) metal

(ii) an alloy and

(iii) a semiconductor

Or

(i) Write the principle of a potentiometer. How can internal resistance of a cell be found with it?

(ii) (a) Why do we prefer a potentiometer with a longer bridge wire?

(b) Why is the use of potentiometer preferred over that of voltmeter?

           

Answer:

Resistivity The resistivity of a metal is equal to the electrical resistance of its wire of unit length and unit area of cross-section. It is denoted by \[\rho \] and its unit is 'ohm-metre'. Temperature dependence of resistivity Resistivity of a metal is given by \[\rho =m/n{{e}^{2}}\tau \] where, m is the mass of an electron, e is charge of an electron, n is electron density and \[\tau \] is relaxation time. With increase in temperature, the average velocity of free electrons increases due to increase in KE and therefore relaxation time \[\tau =\lambda /v,\] decreases. As a result, the resistivity of a metal increases. Therefore, the resistivity of metal increases with increase in temperature. (i) For the metals On the basis of above explanation the graph between resistivity and temperature can be plotted as 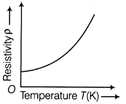(ii) For the alloys Temperature coefficient of resistivity for an alloy is very small and therefore resistivity of an alloy increase very slowly with increases in temperature. 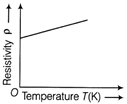(iii) For the semiconductor Resistivity of a semiconductor decreases with increase in temperature. 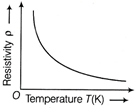Or (i) Principle of potentiometer When an electric current flows through a wire of uniform cross-section area, then potential drop through it, is directly proportional to its length, i.e. \[V\propto l\] or V=Kl where, K is the potential gradient. Measurement of internal resistance of a cell First of all, key \[{{K}_{1}}\] is kept ON and key \[{{K}_{2}}\]  is kept OFF. If no deflection in galvanometer is obtained at length \[{{l}_{1}}\] on wire AB, 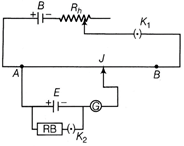Potentiometer internal resistance i.e.        \[A{{J}_{1}}={{l}_{1}}\] Then, emf of the cell,\[E=K{{I}_{1}}\]                 ?(i) Now, key \[{{K}_{2}}\] is also kept ON and a resistance R is applied through resistance box. If no deflection in galvanometer is obtained at length \[{{l}_{2}},\] i.e. \[A{{J}_{2}}={{l}_{2}},\] then terminal potential difference of the cell,             \[V=K{{l}_{2}}\]                                              ?(ii) Dividing Eq. (i) by Eq. (ii), we get             \[\frac{E}{V}=\frac{{{l}_{1}}}{{{l}_{2}}}\]                                         ?(iii) The internal resistance of the cell \[r=\left( \frac{E}{V}-1 \right)R\] Using Eq. (iii), we get \[r=\left( \frac{{{l}_{1}}}{{{l}_{2}}}-1 \right)R\] (ii) (a) In a potentiometer, we read null point. In reading the null point, there can be a maximum error.   \[\text{=}\frac{\text{Emf}\,\,\text{of}\,\,\text{the}\,\,\text{battery}}{\text{Lengh}\,\,\text{of}\,\,\text{the}\,\,\text{wire}}\] The maximum error can be reduced by using longer bridge wire. So, longer bridge wire is used in potentiometer. (b) When potential difference is measured by a voltmeter, a part of current flows through it due to its own resistance. Therefore, measured potential difference is always less than the actual value of potential difference while potentiometer shows no deflection (no deflection condition), i.e. no current flows through the circuit and therefore it measures actual value of the potential difference. That is why potentiometer is preferred over a voltmeter.