Answer:
Radioactive decay law The rate of decay of radioactive nuclei is directly proportional to the number of undecayed nuclei at that time. i.e. \[-\frac{dN}{dt}\propto N\] or \[\frac{dN}{dt}=-\lambda N\] where, \[\lambda \] is the decay constant. \[\frac{dN}{dt}=-\lambda N\Rightarrow \frac{dN}{N}=-\lambda t\] On integrating both sides, we get \[{{\log }_{e}}N=-\lambda t+C\] where, C is a constant of integration. If \[{{N}_{0}}\] is initial number of radioactive nuclei at t = 0, So, \[{{\log }_{e}}{{N}_{0}}=0+C\Rightarrow C={{\log }_{e}}{{N}_{0}}\] Substituting this in Eq. (ii), we get \[{{\log }_{e}}N=-\lambda t+{{\log }_{e}}{{N}_{0}}\] \[\Rightarrow \] \[{{\log }_{e}}N-{{\log }_{e}}{{N}_{0}}=-\lambda t\] \[\Rightarrow \] \[{{\log }_{e}}\frac{N}{N}=-\lambda t\] \[\Rightarrow \] \[\frac{N}{{{N}_{0}}}={{e}^{-\lambda t}}\] \[\Rightarrow \] \[N={{N}_{0}}{{e}^{-\lambda t}}.\] The graph of N as a function of time is shown in figure below. 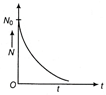
You need to login to perform this action.
You will be redirected in
3 sec
