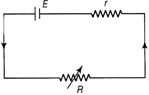
| (i) E with R |
| (ii) terminal potential difference of the cell if with R. |
| Or |
| Distance between the plates of a capacitor of capacitance C is d. A very thin metal sheet is placed as shown in the figure. Calculate the new capacitance. |
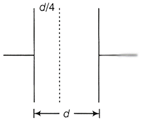 Plate capacitor
Plate capacitor
Answer:
(i) The emf of a cell is independent of the external resistance R. Therefore, graph between E and R will be a straight line parallel to R-axis. 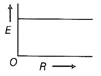 (ii) Terminal potential difference of a cell \[V=IR=\left( \frac{E}{R+r} \right)R=\frac{E}{\left( 1+\frac{r}{R} \right)}\] When the external resistance R increases, r/R decreases and therefore terminal potential difference of the cell increases. Therefore, graph between E and R will be a curve as shown below.
(ii) Terminal potential difference of a cell \[V=IR=\left( \frac{E}{R+r} \right)R=\frac{E}{\left( 1+\frac{r}{R} \right)}\] When the external resistance R increases, r/R decreases and therefore terminal potential difference of the cell increases. Therefore, graph between E and R will be a curve as shown below. 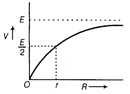 When R = 0, \[V=\frac{E}{1+(r/0)}=0\] When R = r, \[V=\frac{E}{1+(r/r)}=\frac{E}{2}\] When \[R=\infty ,\] ss Or Now, the capacitor will act as a combination of two capacitors connected in series.
When R = 0, \[V=\frac{E}{1+(r/0)}=0\] When R = r, \[V=\frac{E}{1+(r/r)}=\frac{E}{2}\] When \[R=\infty ,\] ss Or Now, the capacitor will act as a combination of two capacitors connected in series. 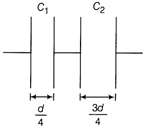 As, \[C\propto \frac{1}{d}\] \[\therefore \] \[{{C}_{1}}=4C\] and \[{{C}_{2}}=4C/3\] \[\therefore \] Equivalent capacitance of the combination, \[\frac{1}{C'}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}}=\frac{1}{4C}+\frac{1}{\frac{4C}{3}}=\frac{1+3}{4C},\] \[\Rightarrow \] \[\frac{1}{C'}=\frac{1}{C}\Rightarrow {{C}^{'}}=C\] Therefore, the capacitance will remain same.
As, \[C\propto \frac{1}{d}\] \[\therefore \] \[{{C}_{1}}=4C\] and \[{{C}_{2}}=4C/3\] \[\therefore \] Equivalent capacitance of the combination, \[\frac{1}{C'}=\frac{1}{{{C}_{1}}}+\frac{1}{{{C}_{2}}}=\frac{1}{4C}+\frac{1}{\frac{4C}{3}}=\frac{1+3}{4C},\] \[\Rightarrow \] \[\frac{1}{C'}=\frac{1}{C}\Rightarrow {{C}^{'}}=C\] Therefore, the capacitance will remain same.
You need to login to perform this action.
You will be redirected in
3 sec
