question_answer

As shown in the figure, a potentiometer with a cell of 2.0V and internal resistance  \[0.5\,\Omega \] maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of 1.1 V (for very moderate currents upto a few A) gives a balance point at 70 cm length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance of \[600k\,\Omega \] is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf e and the balance point found similarly turns out to be at 85cm length of the wire. 4

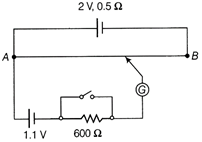
(i) What is the value of\[\varepsilon ?\]

(ii) What purpose does the high resistance of \[600\,k\,\Omega \] have?

(iii) Is the balance point affected by this high resistance?

(iv) Is the balance point affected by the internal resistance of the driver cell?

(v) Would the method work in the above situation, if the driver cell of the potentiometer had an emf of 1.0 V instead of 2.0 V?

(vi) Would the circuit work well for determining extremely small emf, say of the order of a few mV (such as the typical emf of a thermocouple)? If not, how will you modify the circuit?

Or

(i) Show that the normal component of electrostatic field has a discontinuity from one side of a charged surface to another given by

\[({{E}_{2}}-{{E}_{1}})\cdot \hat{n}=\frac{S}{{{\varepsilon }_{0}}}\]

where, \[\hat{n}\] is a unit vector normal to the surface at a. point and \[\sigma \]  is the surface charge density at the point. (The direction of \[\hat{n}\] is from side 1 to side 2). Hence, show that just outside a conductor, the electric field is \[\sigma \hat{n}/{{\varepsilon }_{0}}.\]

(ii) Show that the tangential component of electrostatic field is continuous from one side of a charged surface to another.

Answer:

(i) \[{{\varepsilon }_{1}}=1.1\,V,\,\,{{l}_{1}}=70\,\,cm,\,\,{{\varepsilon }_{2}}=\varepsilon =?,\,\,=85\,\,cm\] Formula for the comparison of emfs by potentiometer is \[\frac{{{\varepsilon }_{2}}}{{{\varepsilon }_{1}}}=\frac{{{l}_{2}}}{{{l}_{1}}}\]             \[\therefore \]                  \[\frac{\varepsilon }{1.1}=\frac{85}{70}\]             Or                     \[\varepsilon =1.1\times \frac{85}{70}=1.33\,V\] (ii) High resistance of \[600\,\,k\Omega \] protects the galvanometer for positions far away from the balance point, by decreasing current through it. (iii) No, balance point is not affected by high resistance, because no current flows through the standard cell at the balance point. (iv) No, the balance point is not affected by the internal resistance of the driver cell as null method is used here. (v) No, the arrangement will not work. If \[\varepsilon \] is greater than the emf of the driver cell of the potentiometer, there will be no balance point on the wire AB. (vi) The circuit as it is would be unsuitable, because the balance point (for \[\varepsilon \] of the order of a few mV) will be very close to the end A and the percentage error in measurement will be very large. The circuit is modified by putting a suitable resistor R in series with the wire AB, so that potential drop across AB is only slightly greater than the emf to be measured. Then, the balance point will be at larger length of the wire and the percentage error will be much smaller. Or (i) Electric field near a plane sheet of charge is given by \[E=\frac{\sigma }{2{{\varepsilon }_{0}}}\] If \[\hat{n}\] is a unit vector normal to the sheet from side 1 to side 2, then electric field on side 2, \[{{E}_{2}}=\frac{\sigma }{2{{\varepsilon }_{0}}}\,\,\hat{n}\] In the direction of the outward normal to the side 2. Similarly, electric field on side 1 is \[{{E}_{1}}=\frac{\sigma }{2{{\varepsilon }_{0}}}\,\,\hat{n}\] In the direction of the outward normal to the side 1. \[\therefore \]      \[({{E}_{2}}-{{E}_{1}})\cdot \hat{n}=\frac{\sigma }{2{{\varepsilon }_{0}}}-\left( \frac{\sigma }{2{{\varepsilon }_{0}}} \right)=\frac{\sigma }{{{\varepsilon }_{0}}}\] As, \[{{E}_{1}}\] and \[{{E}_{2}}\] act in opposite directions, there must be discontinuity at the sheet of charge. Now, electric field vanishes inside a conductor, therefore \[{{E}_{1}}=0\] Hence, outside the conductor, the electric field is \[E={{E}_{2}}=\frac{\sigma }{{{\varepsilon }_{0}}}\,\,\hat{n}\] (ii) Let XY be the charged surface of a dielectric and \[{{E}_{1}}\] and \[{{E}_{2}}\] be the electric fields on the two sides of the charged surface as shown in figure. 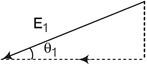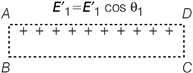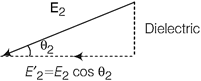Consider a rectangular loop ABCD with length l and negligibly small breadth. Line integral along the closed path ABCD will be \[\int{E.d\,\,l={{E}_{1}}.l-{{E}_{2}}.l=0}\] \[{{E}_{1}}l\cos \,{{\theta }_{1}}-{{E}_{2}}l\cos \,{{\theta }_{2}}=0\] \[({{E}_{1}}\cos \,{{\theta }_{1}}-{{E}_{2}}\cos \,{{\theta }_{2}})\,l=0\] \[(E_{1}^{_{'}}-E_{2}^{_{'}})\,l=0\] Where, \[E_{1}^{'}\] and \[E_{2}^{'}\] are the tangential components of \[{{E}_{1}}\] and \[{{E}_{2}},\] respectively. Thus, \[E_{1}^{_{'}}=E_{2}^{_{'}}\]                      \[(\therefore \,\,l\ne 0)\] Hence, the tangential component of the electrostatic field is continuous across the surface.