question_answer

A boat crosses a river from port A to port B, which are just on the opposite side. The speed of the water is \[{{V}_{W}}\] and that of boat is \[{{V}_{B}}\] relative to still water. Assume\[{{V}_{B}}=2{{V}_{W}}\]. What is the time taken by the boat, if it has to cross the river directly on the AB line?

A) \[\frac{2D}{{{V}_{B}}\sqrt{3}}\]                      

B) \[\frac{\sqrt{3}D}{2{{V}_{B}}}\]

C) \[\frac{D}{{{V}_{B}}\sqrt{2}}\]                        

D) \[\frac{D\sqrt{2}}{{{V}_{B}}}\]

Correct Answer: A

Solution :

From figure, \[{{V}_{B}}\text{ }sin\,\theta \,\,=\,\,{{V}_{W}}\]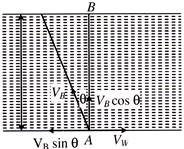   \[\sin \,\theta \,=\,\frac{{{V}_{W}}}{{{V}_{B}}}\,=\,\frac{1}{2}\,\,\Rightarrow \,\,\theta =30{}^\circ \,\,\,\,\,\,\,\,\,\,[\because \,\,{{V}_{B}}=2{{V}_{W}}]\] Time taken to cross the river, \[t=\frac{D}{{{V}_{B}}\cos \,\theta }=\frac{D}{{{V}_{B}}\,\cos \,30{}^\circ }=\frac{2D}{{{V}_{B}}\,\sqrt{3}}\]