A) \[\frac{2{{m}_{1}}{{m}_{3}}g}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]
B) \[\frac{2{{m}_{1}}{{m}_{2}}g}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]
C) \[\frac{4{{m}_{1}}{{m}_{2}}g}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}}\]
D) zero
Correct Answer: D
Solution :
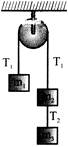
Acceleration \[a=\left( \frac{{{m}_{3}}+{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}} \right)\,g\] for mass \[{{m}_{3}}\,\,{{m}_{3}}g-{{T}_{2}}={{m}_{3}}a\] \[\Rightarrow \] \[{{T}_{2}}={{m}_{3}}g-{{m}_{3}}\left( \frac{{{m}_{3}}+{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}} \right)g\] \[\Rightarrow \]\[{{T}_{2}}=\left( \frac{2{{m}_{1}}{{m}_{2}}g}{{{m}_{1}}+{{m}_{2}}+{{m}_{3}}} \right)\] or Put \[{{m}_{2}}=0\] then \[{{T}_{2}}=\left( \frac{2{{m}_{1}}+{{m}_{3}}}{{{m}_{1}}+{{m}_{3}}} \right)\,g\]You need to login to perform this action.
You will be redirected in
3 sec
