question_answer

In the figure shown, for an angle of incidence \[{{45}^{o}},\]at the top surface, what is the minimum refractive index needed for total internal reflection at vertical face:-                                                   

A)  \[\frac{\sqrt{2}+1}{2}\]

B)  \[\sqrt{\frac{3}{2}}\]

C)  \[\sqrt{\frac{1}{2}}\]

D)  \[\sqrt{2}+1\]

Correct Answer: B

Solution :

At point A, by Snell's law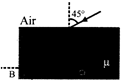 \[\mu =\frac{\sin 45}{\sin r}\Rightarrow \sin r=\frac{1}{\mu \sqrt{2}}\]         ??.(i) At point B, for total internal reflection \[\sin {{i}_{1}}=\frac{1}{\mu }\] From figure, \[{{i}_{1}}=90-r\] \[\therefore \]   \[sin\,({{90}^{o}}-r)=\frac{1}{\mu }\] \[\Rightarrow \]   \[\cos \,\,r=\frac{1}{\mu }\]            ???.(ii) Now \[\cos r=\sqrt{1-{{\sin }^{2}}r}=\sqrt{1-\frac{1}{2{{\mu }_{2}}}}\] \[=\sqrt{\frac{2{{\mu }^{2}}-1}{2{{\mu }^{2}}}}\] ??(iii) From equation (ii) and (iii) \[\frac{1}{\mu }=\sqrt{\frac{2{{\mu }^{2}}-1}{2{{\mu }^{2}}}}\] Squaring both side and then solving we get \[\mu =\sqrt{\frac{3}{2}}\]