A) \[\frac{2D}{{{v}_{B}}\sqrt{3}}\]
B) \[\frac{\sqrt{3}D}{2{{v}_{B}}}\]
C) \[\frac{D}{{{v}_{B}}\sqrt{2}}\]
D) \[\frac{D\sqrt{2}}{{{v}_{B}}}\]
Correct Answer: A
Solution :
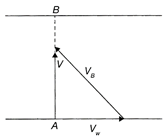 Where b is the velocity of boat with respect to ground Let the time to cross the river bet t \[t=\frac{D}{v}=\frac{D}{\sqrt{v_{B}^{2}-v_{w}^{2}}}=\frac{D}{\sqrt{v_{B}^{2}-{{\left( \frac{{{v}_{B}}}{2} \right)}^{2}}}}\] \[\therefore \] \[t=\frac{2D}{{{v}_{B}}\sqrt{3}}\] Hence, the correction option is (a).
Where b is the velocity of boat with respect to ground Let the time to cross the river bet t \[t=\frac{D}{v}=\frac{D}{\sqrt{v_{B}^{2}-v_{w}^{2}}}=\frac{D}{\sqrt{v_{B}^{2}-{{\left( \frac{{{v}_{B}}}{2} \right)}^{2}}}}\] \[\therefore \] \[t=\frac{2D}{{{v}_{B}}\sqrt{3}}\] Hence, the correction option is (a).
You need to login to perform this action.
You will be redirected in
3 sec
