question_answer

A man wants to reach point B on the opposite bank of a river flowing at a speed as shown in the figure. What minimum speed relative to water should the man have so that he can reach point B?

A) \[u\sqrt{2}\]                            

B) \[\frac{u}{\sqrt{2}}\]

C) \[2u\]                            

D) \[\frac{u}{2}\]

Correct Answer: B

Solution :

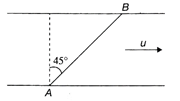
Let v be the speed of boatman in still water.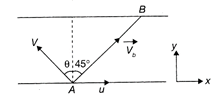 Resultant of v and u should be along AB. Components of\[{{\vec{v}}_{b}}\](absolute velocity of boatman) along\[x\]and y Direction are, \[{{v}_{x}}=u-v\sin \theta \] and \[{{v}_{y}}=v\cos \theta \] Further, \[\tan {{45}^{o}}=\frac{{{v}_{y}}}{{{v}_{x}}}\] or \[1=\frac{v\cos \theta }{u-v\sin \theta }\] \[v=\frac{u}{\sin \theta +\cos \theta }=\frac{u}{\sqrt{2}\sin (\theta +{{45}^{o}})}\] v is minimum at, \[\theta +{{45}^{o}}={{90}^{o}}\]or \[\theta ={{45}^{o}}\] and \[{{v}_{\min }}=\frac{u}{\sqrt{2}}\]