question_answer

An impulse J is applied on a ring of mass m along a line passing through its center O. The ring is placed on a rough horizontal surface. The linear velocity of center of ring once it starts rolling without slipping is

A) \[J/m\]             

B) \[J/2m\]           

C)      \[J/4m\]           

D)      \[J/3m\] 

Correct Answer: B

Solution :

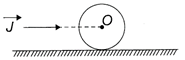
Let v be the velocity of COM of ring just after the impulse is applied and v its velocity when pure rolling starts. Angular velocity co of the ring at this instant will be \[\omega =\frac{v}{r}\]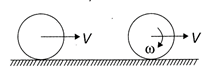 From impulse = change in linear momentum be have J = mv or v = J/m                                           (1) Between the two positions shown in figure force of friction on the ring acts backwards. Angular momentum of the ring about bottommost point will remain conserved as the force of friction always passes through this point. \[\therefore \]    \[{{L}_{1}}={{L}_{f}}\] or \[mvr=mv'r+l\omega \] \[=mv'r+(m{{r}^{2}})\frac{v'}{r}=2mv'r\] \[\therefore \]\[v'=\frac{v}{2}=J/2m\]                        [from eq. (1) Hence, the correction option is (b).