question_answer

A uniform rod of length 2L is placed with one end in contact with the horizontal and is then inclined at an angle a to the horizontal and allowed to fall without slipping at contact point When it becomes horizontal, its angular velocity will be

A) \[\omega =\sqrt{\frac{3g\sin \alpha }{2L}}\]

B) \[\omega =\sqrt{\frac{2L}{3g\,\sin \alpha }}\]

C)      \[\omega =\sqrt{\frac{6g\sin \alpha }{L}}\]

D)      \[\omega =\sqrt{\frac{L}{g\sin \alpha }}\]

Correct Answer: A

Solution :

By the law of conservation of energy, P.E. of rod = rotational K.E.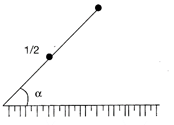 \[mg\frac{l}{2}\sin \propto \frac{1}{2}{{\omega }^{2}}=\frac{1}{2}.\frac{m{{l}^{2}}}{3}{{\omega }^{2}}\] or         \[\omega =\sqrt{\frac{3g\sin \propto }{l}}\] Putting \[1=2L,\,\omega =\sqrt{\frac{3g\sin \propto }{2L}}\] Hence, the correction option is (a).