A) 100, 50
B) 50, 100
C) 0, 100
D) 0, 50
Correct Answer: D
Solution :
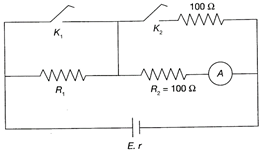
When\[{{K}_{1}}\]is closed, the resistance\[{{R}_{1}}\]is ineffective, Applying kirchoff's voltage law with\[{{k}_{1}}\]closed and\[{{K}_{2}}\]open, while moving through \[{{k}_{1}},{{k}_{2}}\]and the battery, we get \[{{I}_{0}}{{R}_{2}}+{{I}_{0}}r-\varepsilon =0\Rightarrow {{I}_{0}}=\frac{\varepsilon }{{{R}_{2}}+r}\] Applying Kirchoff?s voltage law with both \[{{k}_{1}}\]and\[{{k}_{2}}\]closed, while moving through \[{{k}_{1}},{{k}_{2}}\] and the battery, we get \[{{I}_{0}}{{R}_{2}}+(2{{I}_{0}})r-\varepsilon =0\Rightarrow {{I}_{0}}=\frac{\varepsilon }{{{R}_{2}}+2r}\] Equating the values of \[{{I}_{0}},\]we get \[\frac{\varepsilon }{{{R}_{2}}+r}=\frac{\varepsilon }{{{R}_{2}}+2r}\Rightarrow r=0\] Applying Kirchoff's voltage law while moving through \[{{R}_{1}},{{k}_{2}}\]and the battery, with \[{{k}_{1}}\] open and\[{{k}_{2}}\]closed, we get \[{{I}_{0}}{{R}_{1}}+\frac{{{I}_{0}}}{2}{{R}_{2}}-\varepsilon +{{I}_{0}}r=0\Rightarrow {{I}_{0}}=\frac{\varepsilon }{{{R}_{1}}+\frac{{{R}_{2}}}{2}+r}\] \[\therefore \] \[\frac{\varepsilon }{{{R}_{1}}+\frac{{{R}_{2}}}{2}+r}=\frac{\varepsilon }{{{R}_{2}}+r}\] \[\Rightarrow \] \[\frac{1}{{{R}_{1}}+50}=\frac{1}{100}\Rightarrow {{R}_{1}}=50\Omega \] Hence, the correction option is [d].You need to login to perform this action.
You will be redirected in
3 sec
