A) 0
B) \[\frac{M{{L}^{2}}}{K}\]
C) \[\sqrt{(MK)}L\]
D) \[\frac{K{{L}^{2}}}{2M}\]
Correct Answer: C
Solution :
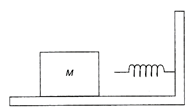
When block of mass M collides with the spring its kinetic energy gets converted into elastic potential energy of the spring. From the law of conservation of energy \[\frac{1}{2}m{{v}^{2}}=\frac{1}{2}K{{L}^{2}},\]\[\therefore \,v=\sqrt{\frac{K}{M}}L.\]so, Its maximum momentum, \[P=Mv=M\sqrt{\frac{K}{M}}L=\sqrt{MK}.L.\] Hence, the correction option is [c].You need to login to perform this action.
You will be redirected in
3 sec
