question_answer

Find the image of the point (1, 6, 3) on the line \[\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}.\]

Also, write the equation of the line joining the given point and its image and find the length of segment joining the given point and its image.

OR

Find the foot of the perpendicular from the point (0, 2, 3) on the line \[\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3}.\]

Also, find the length of the perpendicular.

Answer:

Given, point P = (1, 6, 3) and equation of line AB is \[\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}.\]

Let T(x, y, z) be the image of the point P(1, 6, 3) and Q be the foot of perpendicular PQ on line AB.

Then,    \[\frac{x}{1}=\frac{y-1}{2}=\frac{z-2}{3}=\lambda \,\,(say)\]

\[\Rightarrow \] \[x=\lambda ,\] \[y=2\lambda +1,\] \[z=3\lambda +2\]

Then, coordinates of \[Q=(\lambda ,\,\,2\lambda +1,\,\,3\lambda +2)\] ...(ii)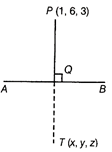

Now, DR's of line

\[PQ=(\lambda -1,\,\,2\lambda +1\,-6,\,\,3\lambda +2-3)\]

\[=(\lambda -1,\,\,2\lambda -5,\,\,3\lambda -1)\]                 ?(iii)

Since, \[PQ\bot AB.\]

\[\therefore \]      \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0\]

Where \[{{a}_{1}}=\lambda -1,\] \[{{b}_{1}}=2\lambda -5,\] \[{{c}_{1}}=3\lambda -1\]

and \[{{a}_{2}}=1,\]\[{{b}_{2}}=2,\] \[{{c}_{2}}=3\]

\[\therefore \]      \[1(\lambda -1)+2(2\lambda -5)+3(3\lambda -1)=0\]

\[\Rightarrow \]   \[\lambda -1+4\lambda -10+9\lambda -3=0\]

\[\Rightarrow \]   \[14\lambda -14=0\] \[\Rightarrow \] \[\lambda =1\]

On putting \[\lambda =1\] in Eq. (ii) we get

Coordinates of \[Q=(1,\text{ }2+1,\text{ }3+2)=\] (1, 3, 5)

Also, Q is the mid-point of PT.

\[\therefore \]      \[Q=\left( \frac{x+1}{2},\,\,\frac{y+6}{2},\,\,\frac{z+3}{2} \right)\]

\[\left[ \begin{align}   & \because \,\,\,\text{mid-point}\,\,\text{of}\,\,({{x}_{1}},\,\,{{y}_{1}}\,\,{{z}_{1}})\,\,and\,\,({{x}_{2}},\,\,{{y}_{2}},\,\,{{z}_{2}}) \\  & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\,\,\frac{{{y}_{1}}+{{y}_{2}}}{2},\,\,\frac{{{z}_{1}}+{{z}_{2}}}{2} \right) \\ \end{align} \right]\]

But       Q = (1, 3, 5)

\[\therefore \]      \[\left( \frac{x+1}{2},\,\,\frac{y+6}{2},\,\,\frac{z+3}{2} \right)\] \[=(1,\,\,3,\,\,5)\]

\[\Rightarrow \]   \[\frac{x+1}{2}=1,\] \[\frac{y+6}{2}=3,\] \[\frac{z+3}{2}=5\]

\[\Rightarrow \]   \[x=2-1,\] \[y=6-6,\] \[z=10-3\]

\[\Rightarrow \]   x = 1, y = 0 and z = 1

So, coordinates of T = (x, y, z) = (1, 0, 7)

Hence, coordinates of image of the point P(1, 6, 3) is T(1, 0, 7).

Length of the segment joining P and T,

\[PT=\sqrt{{{(1-1)}^{2}}+{{(0-6)}^{2}}+{{(7-3)}^{2}}}\]

\[=\sqrt{0+36+16}\] \[=\sqrt{52}=2\sqrt{13}\] units

DR's of line \[PT=(0,\,\,-\,6,\,\,4)\]

DR's of line \[PQ=[1-1,\,\,2(1)-5,\,\,3(1)-1]\]

[from Eq. (iii)]

\[=(0,\,\,-3,\,\,2)\]

Hence, the equation of line PT is

\[\frac{x-1}{0}=\frac{y-6}{-\,3}=\frac{z-3}{2}.\]

OR

Let L be the foot of the perpendicular drawn from the point P(0, 2, 3) to the given line. The coordinates of a general point on the line \[\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3}\] are given by

or, \[x=5\lambda -3,\] \[y=2\lambda +1,\] \[z=3\lambda -4.\]

Let the coordinates of L be \[(5\lambda -3,\,\,2\lambda +1,\,\,3\lambda -4).\] Therefore, direction ratios of PL are proportional to \[5\lambda -3-0,\] \[2\lambda +1-2,\] \[3\lambda -4-3\] i.e.  \[5\lambda -3,\] \[2\lambda -1,\] \[3\lambda -7.\]

\[\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3},\] \[L(5\lambda -3,\,\,2\lambda +1,\,\,3\lambda -4)\]

Direction ratios of the given line are proportional to 5, 2, 3. But, PL is perpendicular to the given line.

\[\therefore \]\[5(5\lambda -3+2(2\lambda -1)+3(3\lambda -7)=0\] \[\Rightarrow \] \[\lambda =1\]

Putting \[\lambda =1\] in \[(5\lambda -3,\,\,2\lambda +1,\,\,3\lambda -4),\] the coordinates of L are \[(2,\,\,3,\,\,-\,1).\]

\[\therefore PL=\sqrt{{{(2-0)}^{2}}+{{(3-2)}^{2}}+{{(-1-3)}^{2}}}=\sqrt{21}\,\,\text{unit}.\]Hence, length of the perpendicular from P on the

given line is \[PL=\sqrt{27}\] units.