| Find the distance of the point \[(-\,2,\,\,3,\,\,-\,4)\] from the line |
| \[\frac{x+2}{3}=\frac{2y+3}{4}=\frac{3z+4}{5}\] measured parallel to the plane \[4x+12y-3z+1=0.\] |
| OR |
| Find the coordinates of foot of perpendicular drawn from the point |
| (0, 2, 3) on the line \[\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3}.\] Also, find the length of perpendicular. |
Answer:
Given point P is \[(-\,2,\,\,3,\,\,-4)\] and equation of line is \[\frac{x+2}{3}=\frac{2y+3}{4}=\frac{3z+4}{5}.\] 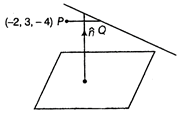
\[4x+12y-3z+1=0\] Let \[\frac{x+2}{3}=\frac{2y+3}{4}=\frac{3z+4}{5}=\lambda \] Then, any point on the line is \[\left( 3\lambda -2,\,\frac{4\lambda -3}{2},\,\,\frac{5\lambda -4}{3} \right).\] Let the coordinates of Q be \[\left( 3\lambda -2,\,\frac{4\lambda -3}{2},\,\,\frac{5\lambda -4}{3} \right)\] DR's of the line PQ are \[3\lambda -2+2,\] \[\frac{4\lambda -3}{2}-3,\] \[\frac{5\lambda -4}{3}+4\] i.e. \[3\lambda ,\] \[\frac{4\lambda -3-6}{2},\] \[\frac{5\lambda -4+12}{3}\] i.e. \[3\lambda ,\] \[\frac{4\lambda -9}{2},\] \[\frac{5\lambda +8}{3}\] Since, line PQ is parallel to the plane \[4x+12y-3z+1=0.\] Therefore, normal to the plane is perpendicular to the line. \[\therefore \] \[4(3\lambda )+12\left( \frac{4\lambda -9}{2} \right)-3\left( \frac{5\lambda +8}{3} \right)=0\] \[[\because \,\,{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0]\] \[\Rightarrow \] \[12\lambda +24\lambda -54-5\lambda -8=0\] \[\Rightarrow \] \[31\lambda -62=0\] \[\Rightarrow \] \[31\lambda =62\] \[\Rightarrow \] \[\lambda =2\] Now, coordinates of point Q \[=\left( 3\times 2-2,\,\,\frac{4\times 2-3}{2},\,\,\frac{5\times 2-4}{3} \right)\] \[[put\,\,\lambda =2]\] \[=\left( 4,\,\,\frac{5}{2},\,\,2 \right)\] Now, distance between P and Q, \[PQ=\sqrt{{{(4+2)}^{2}}+{{\left( \frac{5}{2}-3 \right)}^{2}}+{{(2+4)}^{2}}}\] \[=\sqrt{{{(6)}^{2}}+{{\left( -\frac{1}{2} \right)}^{2}}+{{(6)}^{2}}}\] \[=\sqrt{36+\frac{1}{4}+36}\] \[=\sqrt{\frac{144+1+144}{4}}\] \[=\sqrt{\frac{289}{4}}=\frac{17}{2}\,\,\text{units}\] OR Given equation of line is \[\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3}\] 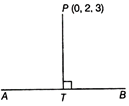
Let \[\frac{x+3}{5}=\frac{y-1}{2}=\frac{z+4}{3}=\lambda \] \[\Rightarrow \] \[\frac{x+3}{5}=\lambda ,\] \[\frac{y-1}{2}=\lambda ,\] \[\frac{z+4}{3}=\lambda \] \[\Rightarrow \] \[x=5\lambda -3,\] \[y=2\lambda +1,\] \[z=3\lambda -4\] Thus, coordinates of any point on the line AB are \[(5\lambda -3,\,\,2\lambda +1,\,\,3\lambda -4).\] Let the coordinates of point T be \[(5\lambda -3,\,\,2\lambda +1,\,\,3\lambda -4)\] Now, DR's of line is \[PT=(5\lambda -3-0,\,\,2\lambda +1-2,\,\,3\lambda -4-3)\] \[=(5\lambda -3,\,\,2\lambda -1,\,\,3\lambda -7)\] \[\because \] \[PT\bot AB\] \[\therefore \] \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0\] Where, \[{{a}_{1}}=5\lambda -3,\,\,{{b}_{1}}=2\lambda -1,\,\,{{c}_{1}}=3\lambda -7\] and \[{{a}_{2}}=5,\,\,{{b}_{2}}=2,\,\,{{c}_{2}}=3\] \[\Rightarrow \] \[5(5\lambda -3)+2(2\lambda -1)+3(3\lambda -7)=0\] \[\Rightarrow \] \[25\lambda -15+4\lambda -2+9\lambda -21=0\] \[\Rightarrow \] \[38\lambda -38=0\] \[\Rightarrow \] \[38\lambda =38\] \[\Rightarrow \] \[\lambda =1\] \[\therefore \] The foot of perpendicular, \[T\equiv (5\lambda -3,\,\,2\lambda +1,\,\,3\lambda -4)\] \[=(2,\,\,3,\,\,-1)\] \[[put\,\,\lambda =1]\] Also, length of perpendicular PT = distance between points P and T, \[PT=\sqrt{{{(0-2)}^{2}}+{{(2-3)}^{2}}+{{(3+1)}^{2}}}\] \[[\because \,\,\,distance=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}]\] \[=\sqrt{4+1+16}=\sqrt{21}\,\,\text{units}\]
You need to login to perform this action.
You will be redirected in
3 sec
