question_answer

If \[\vec{a},\] \[\vec{b},\] and \[\vec{c}\] determine the vertices of a triangle, show that \[\frac{1}{2}[\vec{b}\times \vec{c}+\vec{c}\times \vec{a}+\vec{a}\times \vec{b}]\] gives the vector area of the triangle. Hence, deduce the condition that the three points \[\vec{a},\] \[\vec{b},\] and \[\vec{c}\] are collinear. Also, find the unit vector normal to the plane of the triangle.

Answer:

Let \[\vec{a},\,\vec{b}\] and \[\vec{c}\] be the vertices of a \[\Delta ABC.\] \[\therefore \]      \[\overrightarrow{AB}=\vec{b}-\vec{a}\] and       \[\overrightarrow{AC}=\vec{c}-\vec{a}\] 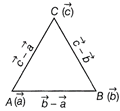                        Now, area of \[\Delta ABC=\frac{1}{2}|\overrightarrow{AB}\,\times \overrightarrow{AC}|\]             \[=\frac{1}{2}\left| \left( \vec{b}-\vec{a} \right)\times \left( \vec{c}-\vec{a} \right) \right|\]             \[=\frac{1}{2}|\vec{b}\times \vec{c}-\vec{b}\times \vec{a}-\vec{a}\times \vec{c}+\vec{a}\times \vec{a}|\]             \[=\frac{1}{2}|\vec{b}\times \vec{c}+\vec{a}\times \vec{b}+\vec{c}\times \vec{a}+\vec{0}|\] \[[\because \vec{b}\times \vec{a}=-\vec{a}\times \vec{b},\,\vec{a}\times \vec{c}=-\vec{c}\times \vec{a}\,\,\text{and}\,\,\vec{a}\times \vec{a}=0]\] \[=\frac{1}{2}|\vec{b}\times \vec{c}+\vec{a}\times \vec{b}+\vec{c}\times \vec{a}|\] Hence, \[\frac{1}{2}[\vec{b}\times \vec{c}+\vec{a}\times \vec{b}+\vec{c}\times \vec{a}]\] gives the vector area of the triangle. If these three points are collinear, the area of \[\Delta ABC\] should be equal to zero. \[\Rightarrow \]   \[\frac{1}{2}[\vec{b}\times \vec{c}+\vec{c}\times \vec{a}+\vec{a}\times \vec{b}]=0\] \[\Rightarrow \]   \[\vec{b}\times \vec{c}+\vec{c}\times \vec{a}+\vec{a}\times \vec{b}=0\] This is the required condition for collinearity of three points \[\vec{a},\,\,\vec{b}\] and \[\vec{c}.\] Let \[\hat{n}\] be the unit vector normal to the plane of the \[\Delta ABC.\] Then, \[\hat{n}=\frac{\overrightarrow{AB}\times \overrightarrow{AC}}{|\overrightarrow{AB}\times \overrightarrow{AC}|}=\frac{(\vec{b}-\vec{a})\times (\vec{c}-\vec{a})}{|(\vec{b}-\vec{a})\times (\vec{c}-\vec{a})|}\]             \[=\frac{\vec{b}\times \vec{c}-\vec{b}\times \vec{a}-\vec{a}\times \vec{c}+\vec{a}\times \vec{a}}{|\vec{b}\times \vec{c}-\vec{b}\times \vec{a}-\vec{a}\times \vec{c}+\vec{a}\times \vec{a}|}\]             \[=\frac{\vec{a}\times \vec{b}+\vec{b}\times \vec{c}+\vec{c}+\vec{a}}{|\vec{a}\times \vec{b}+\vec{b}\times \vec{c}+\vec{c}\times \vec{a}|}\]