question_answer

Find the image of line

\[\frac{x-1}{3}=\frac{y-3}{1}=\frac{z-4}{-\,5}\] in the plane \[2x-y+z+3=0.\]

OR

Find the distance of the point (3, 4, 5) from the plane \[x+y+z=2\] measured parallel to the line\[2x=y=z\].

Answer:

Given equation of the line is

\[\frac{x-1}{3}=\frac{y-3}{1}=\frac{z-4}{-\,5}\]                        ?(i)

and the given plane is

\[2x-y+z+3=0\]

The DR's of line (i) are \[(3,\,\,1,\,\,-5)\] and the DR's of normal to the plane (ii) are \[(2,\,\,-1,\,\,1).\]

Now, by using \[{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}=0,\]  we get

\[(3)(2)+(1)(-1)+(-\,5)(1)=0\]

\[\Rightarrow \]   \[6-1-5=0\] \[\Rightarrow \] 0 = 0

Also, putting x =1, y = 3 and z = 4 in LHS of Eq. (ii), we get

\[LHS=2(1)-(3)+(4)+3=2-3+4+3=6\ne 0\]

\[\therefore \] The point P(1, 3, 4) of line (i) does not lie in the plane (ii).

Hence, line (i) is parallel to the plane (ii).

\[\therefore \] DR's of the line normal to plane (ii) is \[(2,\,\,-1,\,\,1).\]

Let \[Q(\alpha ,\,\,\beta ,\,\,\gamma )\] be the image of the point P(1, 3, 4).

Now, equation of line PM passing through (1, 3, 4) and normal to plane (ii) is

\[\frac{x-1}{2}=\frac{y-3}{-\,1}=\frac{z-4}{1}=\lambda \,\,(say)\]

\[\Rightarrow \]   \[x=2\lambda +1,\] \[y=-\,\lambda +3,\] \[z=\lambda +4\]

\[\therefore \] Any point M on the line

\[=(2\lambda +1),\] \[(-\,\lambda +3),\]\[(\lambda +4)\]     ?(iii)

Since, the point M lies on the plane (ii).

\[\therefore \]      \[=2(2\lambda +1)-\,1(-\,\lambda +3)+\lambda +4+3=0\]

\[\Rightarrow \]   \[4\lambda +2+\lambda -3+\lambda +4+3=0\]

\[\Rightarrow \]   \[6\lambda +6=0\]

\[\Rightarrow \]   \[\lambda =-\,1\]

On putting the value of \[\lambda \] in Eq. (iii), we get'

Coordinates of

\[m=(-\,2+1,\,\,1+3,\,\,-\,1+4)=(-\,1,\,\,4,\,\,3)\]

Since, M is the mid-point of line PQ.

\[\therefore \]      \[(-\,1,\,\,4,\,\,3)=\left( \frac{\alpha +1}{2},\,\,\frac{\beta +3}{2},\,\,\frac{\gamma +4}{2} \right)\]

Then, comparing the corresponding coordinate, we get

\[\frac{\alpha +1}{2}=-\,1\] \[\Rightarrow \] \[\alpha +1=-\,2\]

\[\Rightarrow \]   \[\alpha =-\,3,\] \[\frac{\beta +3}{2}=4\] \[\Rightarrow \] \[\beta +3=8\]

\[\Rightarrow \]   \[\beta =8-3=5\] and \[\frac{\gamma +4}{2}=3\]

\[\Rightarrow \]   \[\gamma +4=6\] \[\Rightarrow \] \[\gamma =2\]

\[\therefore \] Coordinates of \[Q=(-\,3,\,\,5,\,\,2)\]

Hence, the equation of line through Q and parallel to the given line (i) is \[\frac{x+3}{3}=\frac{y-5}{1}=\frac{z-2}{-\,5},\] which is the required Image of line (i).

OR

Given, point = (3, 4, 5)

Equation of plane is\[x+y+z=2\]               ...(i)

and equation of line is \[2x=y=z\]

\[\Rightarrow \]   \[\frac{x}{1}=\frac{y}{2}=\frac{z}{2}\]                           ?(ii)

Let the equation of the line passing through the point (3, 4, 5) and parallel to the line (ii) be

\[\frac{x-3}{1}=\frac{y-4}{2}=\frac{z-5}{2}=\lambda \,(say)\]     ?(iii)

Then, any point A on the line (iii) is

\[A(\lambda +3,\,\,2\lambda +4,\,\,2\lambda +5)\]

If the point \[A(\lambda +3,\,\,2\lambda +4,\,\,2\lambda +5)\] lies on the plane (i), then \[(\lambda +3)+(2\lambda +4)+(2\lambda +5)=2\]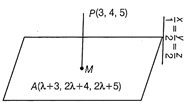

\[\Rightarrow \] \[5\lambda +12=2\,\,\,\,\,\Rightarrow \,\,\,\,\,5\lambda =-\,10\,\,\,\,\,\Rightarrow \,\,\,\,\,\lambda =-\,2\]

On substituting the value of \[\lambda \] in Eq. (iv), we get the coordinates of the point

\[A(-\,2+3,\,\,-\,4+4,-\,4+5),\] i.e. \[A(1,\,\,0,\,\,1)\]

Now, distance between the points

P(3, 4, 5)and A(1, 0, 1)

\[=\sqrt{{{(3-1)}^{2}}+{{(4-0)}^{2}}+{{(5-1)}^{2}}}\]

\[=\sqrt{4+16+16}\]

\[=\sqrt{36}=6\]

Hence, the required distance of the point P(3, 4, 5)from the plane \[x+y+z=2\] measured parallel to the line \[2x=y=z\] is 6 units.