question_answer

Find the area of the circle \[{{x}^{2}}+{{y}^{2}}=16,\] which is exterior to the parabola \[{{y}^{2}}=6x,\] by using integration.

Answer:

Given equation of circle is \[{{x}^{2}}+{{y}^{2}}=16,\]              ?(i) whose centre = (0, 0) and radius = 4 \[\Rightarrow \]   \[y=\pm \sqrt{16-{{x}^{2}}}\] and given equation of parabola is \[{{y}^{2}}=6x\]    ?(ii) \[\Rightarrow \]   \[y=\pm \sqrt{6x}\] On putting the value of \[{{y}^{2}}\] from Eq. (ii) in Eq. (i), we get             \[{{x}^{2}}+6x=16\] \[\Rightarrow \] \[{{x}^{2}}+6x-16=0\] \[\Rightarrow \]   \[{{x}^{2}}+8x-2x-16=0\] \[\Rightarrow \]   \[x(x\,+8)-2(x\,+8)=0\] \[\Rightarrow \]   \[(x+8)(x-2)=0\] \[\Rightarrow \] \[x=2,-\,8\] But \[x=-\,8\] does not satisfy the given curve. \[\therefore \]      x = 2 Then, from Eq. (ii),             \[{{y}^{2}}=6(2)=12\] \[\Rightarrow \] \[y=\pm \sqrt{12}=\pm \,2\sqrt{3}\] Thus, parabola cut the circle at points \[(2,\,\,2\sqrt{3})\] and \[(2,\,\,-2\sqrt{3}).\] 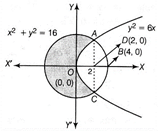            Clearly, area of the region bounded by circle and parabola = Area of OABCO = Area of OADCO + Area of ABCDA \[={{A}_{1}}+{{A}_{2}}(say)\] Now,     \[{{A}_{1}}=2\int_{0}^{2}{{{y}_{(Parabola)}}dx}\]             \[=2\int_{0}^{2}{\sqrt{6x}\,\,dx=2\sqrt{6}\int_{0}^{2}{{{x}^{1/2}}}}dx\]             \[=2\sqrt{6}\left[ \frac{{{x}^{3/2}}}{3/2} \right]_{0}^{2}=2\sqrt{6}\cdot \frac{2}{3}({{2}^{3/2}}-0)\]            \[=\frac{4}{3}\sqrt{6}\cdot 2\sqrt{2}=\frac{8}{3}\sqrt{12}=\frac{8}{3}\times 2\sqrt{3}\]             \[=\frac{16}{3}\sqrt{3}\,\,\text{sq}\,\,\text{units}\] And \[{{A}_{2}}=2{{\int_{2}^{4}{y}}_{(Circle)}}dx=2\int_{2}^{4}{\sqrt{16-{{x}^{2}}}}dx\] \[=2\int_{2}^{4}{\sqrt{{{4}^{2}}-{{x}^{2}}}}dx=2\left[ \frac{x}{2}\sqrt{16-{{x}^{2}}}+\frac{{{4}^{2}}}{2}{{\sin }^{-1}}\frac{x}{4} \right]_{2}^{4}\] \[\left[ \because \,\,\int{\sqrt{{{a}^{2}}-{{x}^{2}}}dx=\frac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\frac{{{a}^{2}}}{2}{{\sin }^{-1}}\frac{x}{a}} \right]\] \[=2\left[ 0+\frac{16}{2}{{\sin }^{-1}}\frac{4}{4}-\frac{2}{2}\sqrt{16-4}-\frac{16}{2}{{\sin }^{-1}}\frac{2}{4} \right]\] \[=2\left[ 8{{\sin }^{-1}}1-\sqrt{12}-8{{\sin }^{-1}}\frac{1}{2} \right]\] \[=2\left[ 8\times \frac{\pi }{2}-2\sqrt{3}-8\times \frac{\pi }{6} \right]\] \[=2\left[ 4\pi -2\sqrt{3}-\frac{4\pi }{3} \right]\] \[=2\left[ \frac{8\pi }{3}-2\sqrt{3} \right]=\left( \frac{16\pi }{3}-4\sqrt{3} \right)\] sq units On putting the values of \[{{A}_{1}}\] and \[{{A}_{2}}\] in Eq. (iii), we get Area of region OABCO, \[A=\frac{16}{3}\sqrt{3}+\frac{16\pi }{3}-4\sqrt{3}\]             \[=\frac{16\pi }{3}+\frac{4}{3}\sqrt{3}\] sq units Hence, area exterior to the parabola = Area of circle \[-\] Area of region OABCO \[=\pi {{(4)}^{2}}-\left( \frac{16\pi }{3}+\frac{4}{3}\sqrt{3} \right)\] \[=16\pi -\frac{16\pi }{3}-\frac{4}{3}\sqrt{3}=\left( \frac{32\pi }{3}+\frac{4}{3}\sqrt{3} \right)\] sq units