question_answer

If \[A=\left[ \begin{matrix}    1 & -1 & 0  \\    2 & 3 & 4  \\    0 & 1 & 2  \\ \end{matrix} \right]\] and \[B=\left[ \begin{matrix}    2 & 2 & 4  \\    -4 & 2 & -4  \\    2 & -1 & 5  \\ \end{matrix} \right],\] find AB. Use this to solve the system of equations

\[x-y=3,\] \[2x+3y+4z=17\] and \[y+2z=7.\]

OR

By using elementary row operations, find the inverse of the matrix \[A=\left[ \begin{matrix}    1 & 3 & -2  \\    -3 & 0 & -5  \\    2 & 5 & 0  \\ \end{matrix} \right].\]

Answer:

We have,

\[AB=\left[ \begin{matrix}    1 & -1 & 0  \\    2 & 3 & 4  \\    0 & 1 & 2  \\ \end{matrix} \right]\,\,\left[ \begin{matrix}    2 & 2 & -\,4  \\    -\,4 & 2 & -\,4  \\    2 & -1 & 5  \\ \end{matrix} \right]\]

\[=\left[ \begin{matrix}    2+4+0 & 2-2+0 & -\,4+4+0  \\    4-12+8 & 4+6-4 & -\,8-12+20  \\    0-4+4 & 0+2-2 & 0-4+10  \\ \end{matrix} \right]\,\]

\[=\left[ \begin{matrix}    6 & 0 & 0  \\    0 & 6 & 0  \\    0 & 0 & 6  \\ \end{matrix} \right]\,\,=6\,\left[ \begin{matrix}    1 & 0 & 0  \\    0 & 1 & 0  \\    0 & 0 & 1  \\ \end{matrix} \right]=6l\]

\[\therefore \]      AB = 6 /                                   ?(i)

Now given system of equations can be written in matrix form as        \[AX=C\] \[\Rightarrow \] \[X={{A}^{-1}}C\]            ? (ii)

Where,\[A=\left[ \begin{matrix}    1 & -1 & 0  \\    2 & 3 & 4  \\    0 & 1 & 2  \\ \end{matrix} \right],\] \[X=\left[ \begin{matrix}    x  \\    y  \\    z  \\ \end{matrix} \right]\] and \[C=\left[ \begin{matrix}    3  \\    17  \\    7  \\ \end{matrix} \right]\]

Now, from Eq, (i) we have

AB = 6 /

\[\Rightarrow \]   \[{{A}^{-1}}(AB)={{A}^{-1}}(6l)\]

[Pre-multiply both sides by \[{{A}^{-1}}\]]

\[\Rightarrow \]   \[({{A}^{-1}}A)B=6({{A}^{-1}}l)\]

\[\Rightarrow \]   \[lB=6{{A}^{-1}}\]

\[[\because \,A{{A}^{-1}}={{A}^{-1}}A=l\,\,\text{and}\,\,Al=A-lA]\]

\[\Rightarrow \]   \[B=6{{A}^{-1}}\]

\[\Rightarrow \]   \[{{A}^{-1}}=\frac{1}{6}B\]

\[\Rightarrow \]   \[{{A}^{-1}}=\frac{1}{6}\,\,\left[ \begin{matrix}    2 & 2 & -\,4  \\    -\,4 & 2 & -\,4  \\    2 & -1 & 5  \\ \end{matrix} \right]\]

Now, from Eq. (ii) we have

\[X={{A}^{-1}}C\]

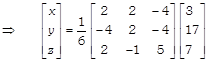
\[\Rightarrow \]   \[\left[ \begin{matrix}    x  \\    y  \\    z  \\ \end{matrix} \right]=\frac{1}{6}\,\,\left[ \begin{matrix}    6 & +\,34 & -\,28  \\    -\,12 & +\,34 & -\,28  \\    6 & -\,17 & +\,35  \\ \end{matrix} \right]\]

\[=\frac{1}{6}\,\,\left[ \begin{matrix}    12  \\    -6  \\    24  \\ \end{matrix} \right]=\left[ \begin{matrix}    2  \\    -1  \\    4  \\ \end{matrix} \right]\]

On comparing corresponding elements, we get

\[x=2,\] \[y=-\,1\] and z = 4

OR

We have,

\[\left[ \begin{matrix}    1 & 3 & -\,2  \\    -\,3 & 0 & -\,5  \\    2 & 5 & 0  \\ \end{matrix} \right]=\left[ \begin{matrix}    1 & 0 & 0  \\    0 & 1 & 0  \\    0 & 0 & 1  \\ \end{matrix} \right]\cdot A\]

\[\Rightarrow \] \[Z=22(0)+18(20)=360\]

\[\left[ \begin{align}   & {{R}_{2}}\to {{R}_{2}}+3{{R}_{1}} \\  & {{R}_{3}}\to {{R}_{3}}-2{{R}_{1}} \\ \end{align} \right]\]

\[\Rightarrow \] \[\left[ \begin{matrix}    1 & 3 & -\,2  \\    0 & -\,1 & 4  \\    0 & 9 & -\,11  \\ \end{matrix} \right]=\left[ \begin{matrix}    1 & 0 & 0  \\    -\,2 & 0 & 1  \\    3 & 1 & 0  \\ \end{matrix} \right]\cdot A\] \[\,\left[ {{R}_{2}}\leftrightarrow {{R}_{1}} \right]\]

\[\Rightarrow \] \[\left[ \begin{matrix}    1 & 0 & 10  \\    0 & -\,1 & 4  \\    0 & 0 & 25  \\ \end{matrix} \right]=\left[ \begin{matrix}    -\,5 & 0 & 3  \\    -\,2 & 0 & 1  \\    -\,15 & 1 & 9  \\ \end{matrix} \right]\cdot A\]

\[\,\,\left[ \begin{matrix}    {{R}_{1}}\to {{R}_{1}}+3{{R}_{2}}  \\    {{R}_{3}}\to {{R}_{3}}+9{{R}_{2}}  \\ \end{matrix} \right]\]

\[\Rightarrow \]\[\left[ \begin{matrix}    1 & 0 & 10  \\    0 & 1 & -\,4  \\    0 & 0 & 25  \\ \end{matrix} \right]=\left[ \begin{matrix}    -\,5 & 0 & 3  \\    2 & 0 & -\,1  \\    -\,15 & 1 & 9  \\ \end{matrix} \right]\cdot A\] \[\left[ {{R}_{2}}\to (-\,1){{R}_{2}} \right]\]

\[\Rightarrow \] \[\left[ \begin{matrix}    1 & 0 & 10  \\    0 & 1 & -\,4  \\    0 & 0 & 1  \\ \end{matrix} \right]=\left[ \begin{matrix}    -\,5 & 0 & 3  \\    2 & 0 & -\,1  \\    -\,3/5 & 1/25 & 9/25  \\ \end{matrix} \right]\cdot A\]

\[\,\left[ {{R}_{3}}\to \frac{1}{25}{{R}_{3}} \right]\]

\[\Rightarrow \] \[\left[ \begin{matrix}    1 & 0 & 0  \\    0 & 1 & 0  \\    0 & 0 & 1  \\ \end{matrix} \right]=\left[ \begin{matrix}    1 & \frac{-\,2}{5} & \frac{-\,3}{5}  \\    \frac{-\,2}{5} & \frac{4}{25} & \frac{11}{25}  \\    \frac{-\,3}{5} & \frac{1}{25} & \frac{9}{25}  \\ \end{matrix} \right]\cdot A\]

\[\left[ \begin{matrix}    {{R}_{1}}\to {{R}_{1}}\to 10{{R}_{3}}  \\   {{R}_{2}}\to {{R}_{2}}\to 4{{R}_{3}}  \\ \end{matrix} \right]\]

Hence, \[{{A}^{-1}}=\left[ \begin{matrix}    1 & \frac{-\,2}{5} & \frac{-\,3}{5}  \\    \frac{-\,2}{5} & \frac{4}{25} & \frac{11}{25}  \\    \frac{-\,3}{5} & \frac{1}{25} & \frac{9}{25}  \\ \end{matrix} \right]\]