question_answer

Find the angle of intersection of the curves \[{{y}^{2}}=x\] and \[{{x}^{2}}=y.\]

OR

A metal box with a square base and vertical sides is to contain \[1024\,\,c{{m}^{3}}.\] If the material for the top and bottom costs Rs.  5 per \[c{{m}^{2}}.\] and the material for the sides Rs. 2.50 per \[c{{m}^{2}}\]. Then, find the least cost of the box.

Answer:

equations of curves are

\[{{y}^{2}}=x\]                                             ? (i)

and       \[{{x}^{2}}=y\]                                              ? (ii)

On solving Eqs. (i) and (ii), we have

\[{{x}^{4}}=x\]

[Substituting the value of y from Eq. (ii) to Eq. (i)]

\[\Rightarrow \]   \[{{x}^{4}}-x=0\] \[\Rightarrow \] \[x({{x}^{3}}-1)=0\]

\[\Rightarrow \]   x = 0 or \[{{x}^{3}}=1\]

\[\Rightarrow \]   x = 0, 1

When x = 0, then y = 0 and when x = 1, then y = 1 Thus, points of intersection are (0, 0) and (1, 1).

Now, consider \[{{y}^{2}}=x\] \[\Rightarrow \] \[2y\frac{dy}{dx}=1\]

\[\Rightarrow \] \[\frac{dy}{dx}=\frac{1}{2y}\]

and       \[{{x}^{2}}=y\]          \[\Rightarrow \] \[\frac{dy}{dx}=2x\]

Now, at (1, 1), slope of tangent to the curve \[{{y}^{2}}=x\] is equal to \[\frac{1}{2}\] and that of \[{{x}^{2}}=y\] is 2.

\[\therefore \]      \[\tan \theta =\left| \frac{2-\frac{1}{2}}{1+2\cdot \frac{1}{2}} \right|=\frac{3}{4}\] \[\Rightarrow \] \[\theta ={{\tan }^{-1}}\frac{3}{4}\]

\[\therefore \]      Angle of intersection is \[{{\tan }^{-1}}\frac{3}{4}.\]

Also, at (0, 0), slope of tangent to the curve \[{{y}^{2}}=x\] is parallel to Y-axis. and that of \[{{x}^{2}}=y\] is parallel to X-axis.

\[\therefore \] Angle of intersection \[=\frac{\pi }{2}\]

OR

Given, volume of the box \[=1024\,\,c{{m}^{3}}.\]

Let length of the side of square base be x cm and height of the box be y cm.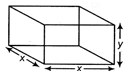

\[\therefore \] Volume of the box (V) \[={{x}^{2}}\cdot y=1024\]

[given]

\[\Rightarrow \]   \[y=\frac{1024}{{{x}^{2}}}\]                          ? (i)

Let C denotes the cost of the box.

\[\therefore \]      \[C=2{{x}^{2}}\times 5+4xy\times 2.50\]

[total area of top and bottom \[=2{{x}^{2}}\] and area of one side = xy]

\[=10{{x}^{2}}+10xy\]

\[=10{{x}^{2}}+10x\left( \frac{1024}{{{x}^{2}}} \right)\]          [from Eq. (i)]

\[\Rightarrow \]   \[C=10{{x}^{2}}+\frac{10240}{{{x}^{2}}}\]               ? (ii)

On differentiating both sides w.r.t. x, we get

\[\frac{dC}{dx}=20x+10240{{(-x)}^{-\,2}}\]

\[=20x-\frac{10240}{{{x}^{2}}}\]                                ? (iii)

Now, for maxima or minima, put \[\frac{dC}{dx}=0\]

\[\Rightarrow \]   \[20x=\frac{10240}{{{x}^{2}}}\] \[\Rightarrow \] \[20{{x}^{3}}=10240\]

\[\Rightarrow \]   \[{{x}^{3}}=512={{8}^{3}}\] \[\Rightarrow \] x = 8

Again, differentiating Eq. (Hi) w.r.t. x, we get

\[\frac{{{d}^{2}}C}{d{{x}^{2}}}=20-10240\,(-\,2)\cdot \frac{1}{{{x}^{3}}}\]

\[=20+\frac{20480}{{{x}^{3}}}\]

Now, \[{{\left( \frac{{{d}^{2}}C}{d{{x}^{2}}} \right)}_{x\,\,=\,\,8}}=20+\frac{20480}{512}=60>0\]

Thus at x = 8, cost is minimum and the corresponding least cost of the box is

\[C(8)=10.{{(8)}^{2}}+\frac{10240}{8}\]           [from Eq. (ii)]               \[=640+1280\]

= Rs. 1920        .