question_answer

Find the vector equation of the line passing through (1, 2, 3) and parallel to the planes \[\vec{r}\cdot (\hat{i}-\hat{j}+2\hat{k})=5\] and \[\vec{r}\cdot (3\hat{i}+\hat{j}+\hat{k})=6.\]

OR

Find the distance of the point \[(1,\,\,-\,2,\,\,3)\] from the plane \[x-y+z=5\] measured parallel to the line

\[\frac{x}{2}=\frac{y}{3}=\frac{z}{-\,6}.\]

Answer:

Consider the required line be parallel to vector \[\overrightarrow{b}\]given by \[\overrightarrow{b}={{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\,\hat{k}\].

The position vector of the point (1, 2, 3) is \[\overrightarrow{a}=\hat{i}+2\hat{j}+3\hat{k}\]

The equation of line passing through (1, 2, 3) and parallel to \[\overrightarrow{b}\]is given by \[\overrightarrow{r}=\overrightarrow{a}+\lambda \vec{b}\]

\[\therefore \]\[\overrightarrow{r}=(\hat{i}+2\hat{j}+3\hat{k})+\lambda \,\,({{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k})\]     ?(i)

The equations of the given planes are

\[\overrightarrow{r}\cdot (\hat{i}-\hat{j}+2\hat{k})=5\]               ?(ii)

and       \[\overrightarrow{r}\cdot (3\,\hat{i}+\hat{j}+\hat{k})=6\]          ?(iii)

The line in Eq. (i) and plane in Eq. (ii) are parallel.

Therefore, the normal to the plane of Eq. (ii) and the given line are perpendicular.

\[\therefore \]      \[(\hat{i}-\hat{j}+2\hat{k})\cdot \lambda \,\,({{b}_{1}}\,\hat{i}+{{b}_{2}}\,\hat{j}+{{b}_{3}}\,\hat{k})=0\]

\[\Rightarrow \]\[\lambda \,\,({{b}_{1}}-{{b}_{2}}+2{{b}_{3}})=0\Rightarrow ({{b}_{1}}-{{b}_{2}}+2{{b}_{3}})=0\]     ?(iv)

Similarly, \[(3\,\hat{i}+\hat{j}+\hat{k})\cdot \lambda \,\,({{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k})=0\]

\[\Rightarrow \]   \[\lambda \,\,(3{{b}_{1}}+{{b}_{2}}+{{b}_{3}})=0\]             ?(v)

From Eqs. (iv) and (v), we get

\[\frac{{{b}_{1}}}{(-\,1)\times 1-1\times 2}=\frac{{{b}_{2}}}{2\times 3-1\times 1}=\frac{{{b}_{3}}}{1\times 1-3\,(-\,1)}\]

\[\Rightarrow \]               \[\frac{{{b}_{1}}}{-\,3}=\frac{{{b}_{2}}}{5}=\frac{{{b}_{3}}}{4}\]

Therefore, the direction ratios of \[\overrightarrow{b}\]are \[-\,3,\]5 and 4.

\[\therefore \]      \[\overrightarrow{b}={{b}_{1}}\hat{i}+{{b}_{2}}\hat{j}+{{b}_{3}}\hat{k}=-\,3\,\hat{i}+5\hat{j}+4\hat{k}\]

On putting the value of \[\overrightarrow{b}\]in Eq. (i), we get

\[\overrightarrow{r}=(\hat{i}+2\hat{j}+3\hat{k})+\lambda \,\,(-\,3\,\hat{i}+5\hat{j}+4\hat{k})\]

Which is the equation of the required line.

OR

Let AB is parallel to the given line.

\[\therefore \]Equation is\[\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-3}{-\,6}\]

General point on the line is

\[B\,(2\lambda +1,\,\,3\lambda -2,\,\,-\,6\lambda +3)\]        ?(i)

If this point lies on the plane, then

\[2\lambda +1-3\lambda +2-6\lambda +3=5\]

\[\Rightarrow \]               \[\lambda =\frac{1}{7}\]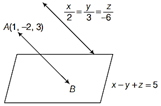

On putting the value of \[\lambda \] in Eq. (i), we get

Point of intersection \[B\,\left( \frac{2}{7}+1,\,\,\frac{3}{7}-2,\,\,-\frac{6}{7}+3 \right)\]

i.e.\[B=\left( \frac{9}{7},-\frac{11}{7},\,\,\frac{15}{7} \right)\]

\[\therefore \]Distance,

\[AB=\sqrt{{{\left( \frac{9}{7}-1 \right)}^{2}}+{{\left( \frac{-\,11}{7}+2 \right)}^{2}}+{{\left( \frac{15}{7}-3 \right)}^{2}}}\]

\[=\sqrt{\frac{4}{49}+\frac{9}{49}+\frac{36}{49}}=\sqrt{1}=1\,\,unit\]