question_answer

Verify Rolle's theorem for the function

\[f(x)=\log \left\{ \frac{{{x}^{2}}+ab}{x(a+b)} \right\}\] on [a, b], where  0<a<b.

OR

Show that the function \[f(x)=\,\,|x+1|+|x-1|,,\] \[\forall \,x\in R\] is not differentiable at the points \[x=-\,1\] and x = 1.

Answer:

Given, \[f(x)=\log \left\{ \frac{{{x}^{2}}+ab}{x(a\,+b)} \right\}\]

\[=\log ({{x}^{2}}+ab)-\log \,x-\log (a\,+b)\]                   ?(i)

\[\left[ \begin{align}   & \because \log \left( \frac{m}{n} \right)=\log m-\log n \\  & \text{and}\,\,\log (ab)=\log a+\log b \\ \end{align} \right]\]

We know that, logarithmic function is differentiable and continuous on its domain. So, f(x) is continuous on [a, b] and differentiable on (a, b).

Now, \[f(a)=\log \left\{ \frac{{{a}^{2}}+ab}{a(a\,+b)} \right\}=\log \,1=0\]

\[f(b)=\log \left\{ \frac{{{b}^{2}}+ab}{b(a\,+b)} \right\}=\log \,1=0\]

\[\therefore \]      \[f(a)=f(b)\]

Thus, all the three conditions of Tolle?s theorem are satisfied.

So, there exists \[c\in (a,\,\,b)\]such that \[f'(c)=0.\]

On differentiating both sides of Eq. (i) w.r.t.x, we get

\[f'(x)=\frac{2x}{{{x}^{2}}+ab}-\frac{1}{x}\]

\[=\frac{2{{x}^{2}}-{{x}^{2}}-ab}{x({{x}^{2}}+ab)}=\frac{{{x}^{2}}-ab}{x({{x}^{2}}+ab)}\]

Put       \[f'(x)=0\] \[\Rightarrow \] \[\frac{{{x}^{2}}-ab}{x({{x}^{2}}+ab)}=0\]

\[\Rightarrow \]   \[{{x}^{2}}=ab\] \[\Rightarrow \] \[x=\pm \,\sqrt{ab}\]

Since, \[a<\sqrt{ab}<b.\] Therefore, \[c=\sqrt{ab}\in (a,\,\,b)\] is such that \[f'(c)=0.\]

Hence, Rolle?s Theorem is verified.

OR

Given, \[f(x)=\,\,|x+1|+|x-1|,\] \[\forall x\in R\]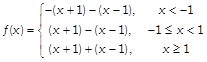

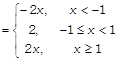
Differentiability at \[x=-1\]

\[Lf'(-\,1)=\underset{h\to \,0}{\mathop{\lim }}\,\frac{f(-\,1-h)-f(-1)}{-\,h}\]

\[=\underset{h\to \,0}{\mathop{\lim }}\,\frac{-\,2(-\,1-h)-2}{-\,h}\]

\[=\underset{h\to \,0}{\mathop{\lim }}\,\frac{2+2h-2}{-\,h}=-\,2\]

\[Rf'(-\,1)=\underset{h\to \,0}{\mathop{\lim }}\,\frac{f(-\,1+h)-f(-\,1)}{h}\]

\[=\underset{h\to \,0}{\mathop{lim}}\,\frac{2-2}{h}=\underset{h\to \,0}{\mathop{\lim }}\,\frac{0}{h}=0\]

\[\because \] \[Lf'(-1)\ne Rf'(-1)\]

\[\therefore \] f(x) is not differentiable at  \[x=-1.\]

Differentiability at x = 1

\[Lf'(1)=\underset{h\to \,0}{\mathop{\lim }}\,\frac{f(1-h)-f(1)}{-h}\]

\[=\underset{h\to \,0}{\mathop{lim}}\,\frac{2-2}{-h}=\underset{h\to \,0}{\mathop{lim}}\,\frac{0}{h}=0\]

and \[Rf'(1)=\underset{h\to \,0}{\mathop{lim}}\,\frac{f(1+h)-f(1)}{h}\]

\[=\underset{h\to \,0}{\mathop{lim}}\,\frac{2(1+h)-2}{h}\]

\[=\underset{h\to \,0}{\mathop{lim}}\,\frac{2+2h-2}{h}\]

\[=\underset{h\to \,0}{\mathop{lim}}\,\frac{2h}{h}=2\]

\[\because \] \[Lf'(1)\ne Rf'(1)\]

\[\therefore \] f(x) is not differentiable at x = 1.

Hence, f(x) is not differentiable at x = 1 and \[-\,1.\]

Hence proved.