question_answer

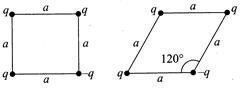
Four point charges q, q, q and \[-q\]are placed at the vertices of a square of side length a. The configuration is changed and the charge are positioned at the vertices of a rhombus of side length a with \[-q\] charge at the vertex where angle is\[120{}^\circ \]. Find the work done by the external agent in changing the configuration.

 

A) \[-\frac{K{{q}^{2}}}{a}\left( 1-\frac{1}{\sqrt{3}} \right)\]           

B)  \[\frac{K{{q}^{2}}}{a}\left( 1+\frac{1}{\sqrt{3}} \right)\]

C) \[-\frac{K{{q}^{2}}}{2a}\left( 1-\frac{1}{\sqrt{3}} \right)\]        

D) \[\frac{K{{q}^{2}}}{2a}\left( 1+\frac{1}{\sqrt{2}} \right)\]

Correct Answer: A

Solution :

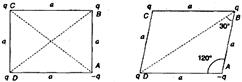
[a] On square: There will be six terms in the expression of potential energy for the system, as there are six pairs of interactions. \[{{U}_{AB}}\] and \[{{U}_{AD}}\] are negative whereas \[{{U}_{BC}}\] and \[{{U}_{CD}}\]positive terms of same magnitude. Similarly \[{{U}_{BD}}\] and \[{{U}_{AC}}\] cancel out. Hence PE is zero.

On Rhombus: \[{{U}_{AB}}\] and \[{{U}_{AD}}\] cancel out with \[{{U}_{BC}}\]and \[{{U}_{CD}}\]. Length \[BD=2a\cos 30{}^\circ =\sqrt{3}a\] \[AC=2a\,\cos 60{}^\circ =a\] \[\therefore \,\,\,\,U={{U}_{BD}}+{{U}_{AC}}\] \[=K\frac{{{q}^{2}}}{\sqrt{3}a}-K\frac{{{q}^{2}}}{a}=-\frac{K{{q}^{2}}}{a}\left( 1-\frac{1}{\sqrt{3}} \right)\] \[\therefore \,\,\,{{W}_{ext\,\,Agt}}={{U}_{\text{Rhombus}}}-{{U}_{square}}=-\frac{K{{q}^{2}}}{a}\left( 1=\frac{1}{\sqrt{3}} \right)\]