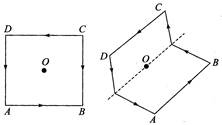
A) \[\frac{{{B}_{0}}}{4}\]
B) \[\frac{{{B}_{0}}}{\sqrt{2}}\]
C) \[2{{B}_{0}}\]
D) Zero
Correct Answer: B
Solution :
[b] \[{{B}_{0}}=\frac{4{{\mu }_{0}}I}{4\pi \frac{L}{2}}(\sin 45{}^\circ +\sin 45{}^\circ )=\frac{2\sqrt{2}{{\mu }_{0}}I}{\pi L}\] After folding \[{{\vec{B}}_{AB}}=\frac{{{\mu }_{0}}I}{4\pi \frac{L}{2}}(\sin 45{}^\circ +\sin 45{}^\circ )\hat{k}=\frac{2\sqrt{2}}{\pi }\frac{{{\mu }_{0}}I}{L}\hat{k}\]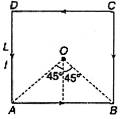 \[{{\vec{B}}_{BE}}=\frac{{{\mu }_{0}}I}{4\pi \frac{L}{2}}(\sin 0{}^\circ +\sin 45{}^\circ )\hat{k}=\frac{\sqrt{2}}{4\pi }\frac{{{\mu }_{0}}I}{L}\hat{k}\] Similarly, we have: \[{{\vec{B}}_{ac}}=\frac{\sqrt{2}{{\mu }_{0}}I}{4\pi L}\hat{i}\]
\[{{\vec{B}}_{BE}}=\frac{{{\mu }_{0}}I}{4\pi \frac{L}{2}}(\sin 0{}^\circ +\sin 45{}^\circ )\hat{k}=\frac{\sqrt{2}}{4\pi }\frac{{{\mu }_{0}}I}{L}\hat{k}\] Similarly, we have: \[{{\vec{B}}_{ac}}=\frac{\sqrt{2}{{\mu }_{0}}I}{4\pi L}\hat{i}\] 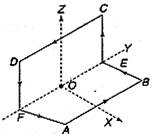 \[{{\vec{B}}_{CD}}=\frac{2\sqrt{2}}{4\pi }\frac{{{\mu }_{0}}I}{L}\hat{i};\]
\[{{\vec{B}}_{CD}}=\frac{2\sqrt{2}}{4\pi }\frac{{{\mu }_{0}}I}{L}\hat{i};\] You need to login to perform this action.
You will be redirected in
3 sec
