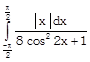has the value
A)
B)
C)
D) none of these
Correct Answer: B
Solution :
Let \[\operatorname{f}(x)=\frac{\left| \,x\, \right|}{8{{\cos }^{2}}2x+1}\] then \[\operatorname{f}(-x)=\frac{\left| -x \right|}{8{{\cos }^{2}}\,2(-x)+1}=\frac{\left| x \right|}{8{{\cos }^{2}}\,2x+1}=f(x)\] \[\therefore \] f(x) is even function \[\therefore \,\,\,I=\int\limits_{\frac{-\pi }{2}}^{\frac{\pi }{2}}{\frac{\left| x \right|\,dx}{8{{\cos }^{2}}2x+1}}=2\int\limits_{0}^{\frac{\pi }{2}}{\frac{\left| x \right|dx}{8\,co{{s}^{2}}2x+1}}\] \[=\,\,2\int\limits_{0}^{\frac{\pi }{2}}{\frac{x\ dx}{8\,co{{s}^{2}}2x+1}}=2\,{{I}_{1}}\] \[\therefore \,\,{{I}_{1}}=\int\limits_{0}^{\frac{\pi }{2}}{\frac{\left( \frac{\pi }{2}-x \right)dx}{8{{\cos }^{2}}2\left( \frac{\pi }{2}-x \right)+1}}=\int\limits_{0}^{\frac{\pi }{2}}{\frac{\frac{\pi }{2}-x}{8{{\cos }^{2}}2x+1}\,dx}\] \[=\,\,\frac{\pi }{2}\,\int\limits_{0}^{\frac{\pi }{2}}{\frac{dx}{8{{\cos }^{2}}2x+1}}-{{I}_{1}}\] \[2{{I}_{1}}=\,\,\frac{\pi }{2}\,\,.\,\,2\int\limits_{0}^{\frac{\pi }{4}}{\frac{dx}{8{{\cos }^{2}}2x+1}}\] \[=\,\,\pi \int\limits_{0}^{\frac{\pi }{4}}{\frac{{{\sec }^{2}}\,2x}{9+{{\tan }^{2}}\,2x}}\,dx\] Put \[\tan \,2x=t\, \Rightarrow 2se{{c}^{2}}\,2x dx = dt\] \[2{{I}_{1}}=\frac{\pi }{2}\int\limits_{2}^{\infty }{\frac{dt}{9+{{t}^{2}}}}=\frac{\pi }{2}.\frac{1}{3}\left[ {{\tan }^{-1}}\frac{t}{3} \right]_{0}^{\infty }=\frac{\pi }{2}.\frac{1}{3}.\frac{\pi }{2}\] \[\therefore \,\,\,{{I}_{1}}=\frac{{{\pi }^{2}}}{24}\Rightarrow \,\,\,I=2\,\,\,{{I}_{1}}=\frac{{{\pi }^{2}}}{12}\]
You need to login to perform this action.
You will be redirected in
3 sec
