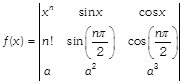question_answer

If , then \[\frac{{{d}^{n}}}{d{{x}^{n}}}\,[f(x)]\] at \[x=0\] is.

A) 2                                 

B) 4

C) 0                                 

D) 8

Correct Answer: C

Solution :

\[\frac{d''[f(x)]}{d{{x}^{n}}}\,\,i.e.\,\,{{f}^{n}}(x)\]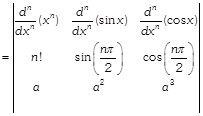      ? (I) [since elements in second and third rows are constants] Let \[y={{x}^{n}}\], then \[{{y}_{1}}=\frac{dy}{dx}=n{{x}^{n-1}},\,\,{{y}_{2}}=\frac{{{d}^{2}}y}{d{{x}^{2}}}=n(n-1){{x}^{n-2}}\],    ...II \[{{y}_{n}}=n(n-1)(n-2)....1.{{x}^{n-n}}=n!\] Again let \[y=sin\,x\], then \[{{y}_{1}}\ =cos\,x=sin\,\left( \frac{\pi }{2}+x \right)\] \[{{y}_{2}}\ =\,\,cos\,\left( \frac{\pi }{2}+x \right)=sin\,\left\{ \frac{\pi }{2}+\left( \frac{\pi }{2}+x \right) \right\}=\sin \left( 2.\frac{\pi }{2}+x \right)\]Proceeding in this way, we get \[{{\operatorname{y}}_{n}}=\,\,sin\,\left( n.\frac{\pi }{2}+x \right)\] Similarly, if \[\operatorname{y} =cos\,x\], then  \[{{\operatorname{y}}_{1}} =-\sin \,x=cos\left( \frac{\pi }{2}+x \right)\] \[{{\operatorname{y}}_{2}}\ =\,\,-\sin \,\left( \frac{\pi }{2}+x \right)=\cos \,\left\{ \frac{\pi }{2}+\left( \frac{\pi }{2}+x \right) \right\}\] \[=\,\,\cos \left( 2.\frac{\pi }{2}+x \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\therefore \,\,{{y}_{n}}=\cos \left( n\,.\frac{\pi }{2}+x \right)\] Thus, \[\frac{{{d}^{n}}}{d{{x}^{n}}}({{x}^{n}})=n!,\,\,\frac{{{d}^{n}}}{d{{x}^{n}}}(sin\,x)=sin\left( x+\frac{n\pi }{2} \right)\] and \[\frac{{{d}^{n}}}{d{{x}^{n}}}(\cos \,x)=\cos \,\left( x+\frac{n\pi }{2} \right)\] From (1), we have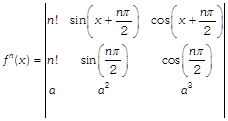 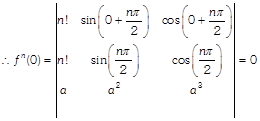\[[\because \,\,\,{{R}_{1}}\,\,and\,\,{{R}_{2}}\,\,are\,\,identical]\]