question_answer

Six point masses each of mass m are placed at the vertices of a regular hexagon of side. The force acting on any of the masses is

A) \[\frac{G{{m}^{2}}}{{{l}^{2}}}\,\left[ \frac{5}{4}+\frac{1}{\sqrt{3}} \right]\]

B) \[\frac{G{{m}^{2}}}{{{l}^{2}}}\,\left[ \frac{3}{4}+\frac{1}{\sqrt{3}} \right]\]

C) \[\frac{G{{m}^{2}}}{{{l}^{2}}}\,\left[ \frac{5}{4}-\frac{1}{\sqrt{3}} \right]\]

D) \[\frac{G{{m}^{2}}}{{{l}^{2}}}\,\left[ \frac{3}{4}-\frac{1}{\sqrt{3}} \right]\]

Correct Answer: A

Solution :

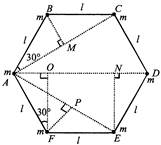
From figure,

\[AC=AM+MC=2AM=\,\,2l\,cos30{}^\circ =2l\frac{\sqrt{3}}{2}=\sqrt{3l}\]

Similarly,\[AE=\sqrt{3}l\],

\[\operatorname{AD} =AO+ON+ND= l sin\,30{}^\circ  + l + l\,\,sin\,\,30{}^\circ \]

\[=\,\,l\times \frac{1}{2}+l+l\times \frac{1}{2}=2\,l\]

\[AB=AF=l\]

Force on mass m at A due to mass m at B is

\[{{F}_{AB}}=\frac{Gmm}{{{(AB)}^{2}}}=\frac{Gmm}{{{l}^{2}}}\,\,along\,\,AB\]

Force on mass m at A due to mass m at C is

\[{{F}_{AC}}=\frac{Gmm}{{{(AC)}^{2}}}=\frac{Gmm}{{{(\sqrt{3l})}^{2}}}\,=\frac{G{{m}^{2}}}{3{{l}^{2}}}\,\,along\,\,AC\]

Force on mass m at A due to mass m at D is

\[{{F}_{AD}}\,\,=\,\,\frac{Gmm}{{{(AD)}^{2}}}\,\,=\,\,\frac{Gmm}{(2\,{{l}^{2}})}\,\,=\,\,\frac{G{{m}^{2}}}{4\,{{l}^{2}}}\,\,along\,\,AD\]

Force on mass m at A due to mass m at E is

\[{{F}_{AE}}\,\,=\,\,\frac{Gmm}{{{(AE)}^{2}}}\,\,=\,\,\frac{Gmm}{{{(\sqrt{3\,l})}^{2}}}\,\,=\,\,\frac{G{{m}^{2}}}{3\,{{l}^{2}}}\,\,along\,\,AE\]

Force on mass m at A due to mass m at F is

\[{{F}_{AF}}\,\,=\,\,\frac{Gmm}{{{(AF)}^{2}}}\,\,=\,\,\frac{G{{m}^{2}}}{{{l}^{2}}}\,\,=\,\,along\,\,AF\]

Resultant force due to \[{{F}_{AB}}\,\,and\,\,{{F}_{AF}}\] is

\[{{F}_{{{R}_{1}}}}=\sqrt{F_{AB}^{3}+F_{AF}^{2}+2{{F}_{AB}}\,{{F}_{AF}}\,\cos \,\,120{}^\circ }\]

\[=\,\,\,\sqrt{\left( \frac{G{{m}^{2}}}{{{l}^{2}}} \right)+\left( \frac{G{{m}^{2}}}{{{l}^{2}}} \right)+2\left( \frac{G{{m}^{2}}}{{{l}^{2}}} \right)\left( \frac{G{{m}^{2}}}{{{l}^{2}}} \right)\left( -\frac{1}{2} \right)}\] \[=\,\,\frac{G{{m}^{2}}}{{{l}^{2}}}\,\,along\,\,AD\]

Resultant force due to \[{{\operatorname{F}}_{AC}}\,\,and\,\,{{F}_{AE}}\] is

\[{{F}_{{{R}_{2}}}}=\sqrt{F_{AC}^{2}+F_{AE}^{2}+2{{F}_{AC}}\,{{F}_{AE}}\,\,\cos \,60{}^\circ }\]

\[=\,\,\,\sqrt{\left( \frac{G{{m}^{2}}}{3{{l}^{2}}} \right)+\left( \frac{G{{m}^{2}}}{3{{l}^{2}}} \right)+2\left( \frac{G{{m}^{2}}}{3{{l}^{2}}} \right)\left( \frac{G{{m}^{2}}}{3{{l}^{2}}} \right)\left( \frac{1}{2} \right)}\]\[=\,\,\frac{\sqrt{3}\,G{{m}^{2}}}{3\,{{l}^{2}}}=\frac{G{{m}^{2}}}{\sqrt{3\,{{l}^{2}}}}\] along AD

Net force on mass m along AD is

\[{{F}_{R}}={{F}_{{{R}_{1}}}}+{{F}_{{{R}_{2}}}}+{{F}_{AD}}\,\,=\,\,\frac{G{{m}^{2}}}{{{l}^{2}}}+\frac{G{{m}^{2}}}{\sqrt{3\,{{l}^{2}}}}+\frac{G{{m}^{2}}}{4\,{{l}^{2}}}\]

\[=\,\,\frac{G{{m}^{2}}}{{{l}^{2}}}\left[ 1+\frac{1}{\sqrt{3}}+\frac{1}{4} \right]=\frac{G{{m}^{2}}}{l{{\,}^{2}}}\,\left[ \frac{5}{4}+\frac{1}{\sqrt{3}} \right]\]