A) The temperature difference across \[A=15{}^\circ C\]
B) The temperature difference across \[A=5{}^\circ C\]
C) The temperature difference across A is \[10{}^\circ C\]
D) The rate of transfer of heat through A is more than that through B.
Correct Answer: B
Solution :
| In series rate of flow of heat is same |
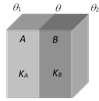 |
| \[\Rightarrow \] \[\frac{{{K}_{A}}A({{\theta }_{1}}-\theta )}{l}=\frac{{{K}_{B}}A(\theta -{{\theta }_{2}})}{l}\] |
| \[\Rightarrow \] \[3{{K}_{B}}({{\theta }_{1}}-\theta )={{K}_{B}}(\theta -{{\theta }_{2}})\] |
| \[\Rightarrow \] \[3({{\theta }_{1}}-\theta )=(\theta -{{\theta }_{2}})\] |
| \[\Rightarrow \] \[3{{\theta }_{1}}-3\theta =\theta -{{\theta }_{2}}\] |
| \[\Rightarrow \] \[4{{\theta }_{1}}-4\theta ={{\theta }_{1}}-{{\theta }_{2}}\] |
| \[\Rightarrow \] \[4({{\theta }_{1}}-\theta )=({{\theta }_{1}}-{{\theta }_{2}})\] |
| \[\Rightarrow \] \[4({{\theta }_{1}}-\theta )=20\] |
| \[\Rightarrow \] \[({{\theta }_{1}}-\theta )=5{}^\circ C\] |
You need to login to perform this action.
You will be redirected in
3 sec
