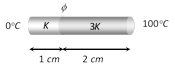
A) \[{{50}^{o}}C\]
B) \[\frac{100}{3}{{\ }^{o}}C\]
C) \[{{60}^{o}}C\]
D) \[\frac{200}{3}{{\ }^{o}}C\]
Correct Answer: C
Solution :
Temperature of interface \[\theta =\frac{{{K}_{1}}{{\theta }_{1}}{{l}_{2}}+{{K}_{2}}{{\theta }_{2}}{{l}_{1}}}{{{K}_{1}}{{l}_{2}}+{{K}_{2}}{{l}_{1}}}\]\[=\frac{K\times 0\times 2+3K\times 100\times 1}{K\times 2+3K\times 1}\] \[=\frac{300K}{5K}\]\[=60{}^\circ C\]You need to login to perform this action.
You will be redirected in
3 sec
