A) 3500 J
B) 350 J
C) 7000 J
D) 750 J
Correct Answer: A
Solution :
| [a] As heat is supplied to gas, it expands against atmospheric pressure and weight of piston. Thus the pressure of gas is constant given by, |
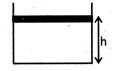 |
| \[P={{P}_{0}}+\frac{mg}{A}\] |
| \[P=1\times {{10}^{5}}+\frac{100\times 10}{4\times {{10}^{-2}}}=\left( 1+\frac{1}{4} \right){{10}^{5}}\] |
| \[=1.25\times {{10}^{5}}N/{{m}^{2}}\] |
| It is given that, |
| \[A=4d{{m}^{2}}=4\times {{10}^{-2}}{{m}^{2}}\] |
| \[m=100kg\] |
| \[n=\text{1mole}\] |
| \[V=\frac{nRT}{P}=2\times {{10}^{-2}}{{m}^{3}}\] |
| Initial height of piston from base of vessel, |
| \[h=\frac{V}{A}=\frac{2\times {{10}^{-2}}}{4\times {{10}^{-2}}}=\frac{1}{2}m\] |
| As process is isobaric, so |
| \[\frac{{{T}_{1}}}{{{T}_{2}}}=\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{V}{V+A\Delta h}=\frac{h}{h+\Delta h}\] |
| \[\therefore \] \[\frac{{{T}_{2}}-{{T}_{1}}}{{{T}_{1}}}=\frac{\Delta h}{h}\] |
| \[\Delta Q=n{{C}_{p}}({{T}_{2}}-{{T}_{1}})=\frac{n.{{C}_{p}}.{{T}_{1}}}{h}\Delta h\] |
| \[=\frac{7}{2}\times \frac{25}{3}\times \frac{300}{0.5}\times 0.2=350\text{0 J}\] |
You need to login to perform this action.
You will be redirected in
3 sec
