A) Rs.108.32
B) Rs.296.28
C) Rs.101.59
D) Rs. 96.28
Correct Answer: D
Solution :
External radius of hemispherical vessel \[{{r}_{1}}=\frac{25}{2}\,cm\]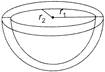 External curved surface area of hemispherical; vessel \[=2\pi \,\,{{r}_{1}}^{2}=2\times \frac{22}{7}\times {{\left( \frac{25}{2} \right)}^{2}}=\frac{6875}{7}\,c{{m}^{2}}\] Internal curved surface area of hemispherical vessel \[=2\pi {{r}_{2}}^{2}\] \[=2\times \frac{22}{7}\times {{12}^{2}}=\frac{6336}{7}c{{m}^{2}}\] Area of top of the hemispherical vessel \[=\pi {{r}_{1}}^{2}-\pi {{r}_{2}}^{2}=\pi \left[ {{\left( \frac{25}{2} \right)}^{2}}-{{12}^{2}} \right]\] \[=\frac{22}{7}\left[ \frac{625-567}{4} \right]=\frac{22}{7}\times \frac{49}{4}=38.5c{{m}^{2}}\] Total surface area of the vessel \[=\frac{6875}{7}+\frac{6336}{7}+38.5=1925.78\,c{{m}^{2}}\] Cost of painting the vessel at the rate of \[Rs.0.05\text{ }per\text{ }c{{m}^{2}}=1925.78\times 0.05=Rs.96.28~\]
External curved surface area of hemispherical; vessel \[=2\pi \,\,{{r}_{1}}^{2}=2\times \frac{22}{7}\times {{\left( \frac{25}{2} \right)}^{2}}=\frac{6875}{7}\,c{{m}^{2}}\] Internal curved surface area of hemispherical vessel \[=2\pi {{r}_{2}}^{2}\] \[=2\times \frac{22}{7}\times {{12}^{2}}=\frac{6336}{7}c{{m}^{2}}\] Area of top of the hemispherical vessel \[=\pi {{r}_{1}}^{2}-\pi {{r}_{2}}^{2}=\pi \left[ {{\left( \frac{25}{2} \right)}^{2}}-{{12}^{2}} \right]\] \[=\frac{22}{7}\left[ \frac{625-567}{4} \right]=\frac{22}{7}\times \frac{49}{4}=38.5c{{m}^{2}}\] Total surface area of the vessel \[=\frac{6875}{7}+\frac{6336}{7}+38.5=1925.78\,c{{m}^{2}}\] Cost of painting the vessel at the rate of \[Rs.0.05\text{ }per\text{ }c{{m}^{2}}=1925.78\times 0.05=Rs.96.28~\]
You need to login to perform this action.
You will be redirected in
3 sec
