question_answer

If OABC is a tetrahedron where O is the origin and A, B, C are three other vertices with position vectors \[\overset{\to }{\mathop{a}}\,,\text{ }\overset{\to }{\mathop{b}}\,\] and \[\overset{\to }{\mathop{c}}\,\] respectively, then the centre of sphere circumscribing the tetrahedron is given by the position vector      

A) \[\frac{{{a}^{2}}(\vec{b}\times \vec{c})+{{b}^{2}}(\vec{c}\times \vec{a})+{{c}^{2}}(\vec{a}\times \vec{b})}{2[\vec{a}\,\vec{b}\,\vec{c}]}\]

B) \[\frac{{{b}^{2}}(\vec{b}\times \vec{c})+{{a}^{2}}(\vec{c}\times \vec{a})+{{c}^{2}}(\vec{a}\times \vec{b})}{[\vec{a}\,\vec{b}\,\vec{c}]}\]

C) \[\frac{{{b}^{2}}(\vec{b}\times \vec{c})+{{a}^{2}}(\vec{c}\times \vec{a})+{{c}^{2}}(\vec{a}\times \vec{b})}{2[\vec{a}\,\vec{b}\,\vec{c}]}\]

D) \[\frac{{{a}^{2}}(\vec{a}\times \vec{b})+{{b}^{2}}(\vec{b}\times \hat{c})+{{c}^{2}}(\vec{c}\times \vec{a})}{2[\vec{a}\,\vec{b}\,\vec{c}]}\]

Correct Answer: A

Solution :

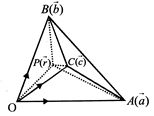
[a] If the centre \['P'\]is with position vector \[\vec{r},\]

Then \[\vec{a}-\vec{r}=\overrightarrow{PA},\vec{b}-\vec{r}=\overrightarrow{PB},\vec{c}-\vec{r}=\overrightarrow{PC,}\]

Where \[\left| \overrightarrow{PA} \right|=\left| \overrightarrow{PB} \right|\]

\[=\left| \overrightarrow{PC} \right|=\left| \overrightarrow{OP} \right|=\left| {\vec{r}} \right|\]

Consider \[\left| \vec{a}-\vec{r} \right|=\left| {\vec{r}} \right|\]

\[\Rightarrow (\vec{a}-\vec{r}).(\vec{a}-\vec{r})=\vec{r}.\vec{r}\]

\[\Rightarrow {{a}^{2}}=-2\vec{a}.\vec{r}+{{r}^{2}}={{r}^{2}}\]

\[\Rightarrow {{a}^{2}}=2\vec{a}.\vec{r}\] Similarly, \[{{b}^{2}}=2\vec{b}.\vec{r}\] and \[{{c}^{2}}\]

\[=2\vec{c}.\vec{r}\]

Since, \[(\vec{b}\times \vec{c}),(\vec{c}\times \vec{a})\] and \[(\vec{a}\times \vec{b})\] are non-coplanar, then

\[\vec{r}=x(\vec{b}\times \vec{c})+y(\vec{c}\times \vec{a})+z(\vec{a}\times \vec{b})\]

\[\vec{a}.\,\vec{r}=x\,\vec{a}.(\vec{b}\times c)+y.0+z.0=x[\vec{a}\,\vec{b}\,\vec{c}]\]

\[\Rightarrow x=\frac{\vec{a}.\vec{r}}{[\vec{a}\,\vec{b}\,\vec{c}]}=\frac{{{a}^{2}}}{2[\vec{a}\,\vec{b}\,\vec{c}]}\]

Similarly, \[y=\frac{{{b}^{2}}}{2[\vec{a}\,\vec{b}\,\vec{c}]}\] and \[z=\frac{{{c}^{2}}}{2[\vec{a}\,\vec{b}\,\vec{c}]}\]

Therefore, \[\vec{r}\]

\[=\frac{{{a}^{2}}(\vec{b}\times \vec{c})+{{b}^{2}}(\vec{c}\times \vec{a})+{{c}^{2}}(\vec{a}\times \vec{b})}{2[\vec{a}\,\vec{b}\,\vec{c}]}\]