question_answer 1)
If a rod is in variable state (not in steady state), then
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 2)
A body cools down from \[{{70}^{o}}C\] to \[{{60}^{o}}\] in 5 min. It will cool down from \[{{100}^{o}}C\] to \[{{90}^{o}}C\] in (Assume cooling by radiation alone)
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 3)
A glass full of hot milk is poured on the table. It begins to cool gradually. Which of the following is incorrect?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 4)
Three discs A, B and C having radii 2 m, 4 m and 6 m respectively on coated with carbon black on their outer surfaces. The wavelength corresponding to maximum intensities are 300 nm, 400 nm and 500 nm respectively. The power radiated by them are \[{{Q}_{A}},\,{{Q}_{B}}\] and \[{{Q}_{C}}\] respectively
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 5)
Water is being boiled in a flat bottom kettle placed on a stove. The area of the bottom is \[3000\text{ }c{{m}^{2}}\] and the thickness is 2 mm. If the amount of steam produced is 1 g/min. Calculate the difference of temperature between the inner and outer surface of the bottom. Thermal conductivity for the material of kettle is \[0.5\,cal/{{\,}^{o}}C/s/cm\] and the latent heat of steam is 540 cal/gm.
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 6)
A ring consisting of two parts ADB and ACB of same conductivity k carries an amount of heat H. The ADB part is now replaced with another metal keeping the temperatures \[{{T}_{1}}\] and \[{{T}_{2}}\] constant. The heat carried increases to 2H. What should be the conductivity of the new ADB part? Given \[\frac{ACB}{ADB}=3\].
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 7)
The emissivity and the surface area of filament of electric bulb are 0.7 and \[5\times {{10}^{-5}}{{m}^{2}}\]. The operating temperature of the filament is 3000 K. The power of the bulb is approximately \[[\sigma =5.67\times {{10}^{-8}}watt/{{m}^{2}}-{{K}^{4}}]\]
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 8)
A rod of length I (laterally thermally insulated) of uniform cross-sectional area A consists of a material whose thermal conductivity varies with temperature as \[K=\frac{{{k}_{0}}}{a+bT},\] where, \[{{k}_{0}},\] a and b are constants. \[{{T}_{1}}\] and \[{{T}_{2}}(<{{T}_{1}})\] are the temperature of two ends of rod. Then, rate of flow of heat across the rod is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 9)
At a specific temperature, the energy densities for a black body for three different wavelengths are 10, 19 and 7 units. For these wavelengths if the absorption coefficient of a body is respectively 0.8, 0.3 and 0.9 then the emissive powers of this body for these wavelengths are in the ratio
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 10)
The two ends of a conducting rod of varying cross. section are maintained at \[\text{20}{{\text{0}}^{\text{o}}}\text{C}\] and \[{{\text{0}}^{\text{o}}}\text{C}\] respectively in steady state
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 11)
Two rods having thermal conductivities in the ratio of 5 : 3 having equal lengths and equal cross-sectional area are joined in series. If the temperature of the free end of the first rod is \[{{100}^{o}}C\] and free end of the second rod is \[{{20}^{o}}C\]. Then temperature of the junction is
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 12)
All the rods have same conductance K and same area of cross section A. If ends A and Care maintained at temperature 2Ty and T respectively then which of the following is/are correct:
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 13)
Direction: In the following questions, more than one of one answers given are correct. Select the correct answers and mark it according to the following codes: Two bodies A and B have thermal emissivities of 0.01 and 0.81 respectively. The outer surface areas of the two bodies are the some. The two bodies emit total radian power at the same rate. The wavelength \[{{\lambda }_{B}}\] corresponding to maximum spectral radiancy in the radiation from B is shifted from the wa9.-velength corresponding to maximum spectral radiancy in the radiation from A, by \[1.00\,\mu m\]. If the temperature of A is 5802 K (1) The temperature of B is 1934 K (2) \[{{\lambda }_{B}}=1.5\,\mu m\] (3) The temperature of B is 11604 K (4) The temperature of B is 2901 K
Codes:
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 14)
Direction: In the following questions, more than one of one answers given are correct. Select the correct answers and mark it according to the following codes: A cane is taken out from a refrigerator at \[0{}^\circ C\]. The atmospheric temperature is \[25{}^\circ C\]. If \[{{t}_{1}}\] is the time taken to heat from \[0{}^\circ C\] to \[5{}^\circ C\] and \[{{t}_{2}}\] is the time taken from \[10{}^\circ C\] to \[15{}^\circ C,\] then the wrong statements are to \[{{15}^{o}}C,~\] then the wrong statements are (1) \[{{t}_{1}}>{{t}_{2}}\] (2) \[{{t}_{1}}={{t}_{2}}\] (3) There is no relation (4) \[{{t}_{1}}<{{t}_{2}}\]
Codes:
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 15)
Direction: In the following questions, more than one of one answers given are correct. Select the correct answers and mark it according to the following codes: The rate of loss of heat from a body cooling under conditions of forced convection is proportional to its (1) surface area (2) excess of temperature over that of surrounding (3) heat capacity (4) absolute temperature
Codes:
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 16)
The maximum spectral emissive power for a black body at temperature 5000K is obtained at\[{{\lambda }_{m}}=6000\overset{o}{\mathop{A}}\,.\] If the temperature is increased by 10% then decrease in \[{{\lambda }_{m}}\] will be (approximately)
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 17)
Find the equivalent thermal resistance of combination of rods as shown in figure. Every rod has same length I and cross-sectional area A. Thermal conductivities are mentioned in figure.
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
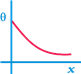
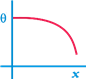
question_answer 18)
A long metallic bar is carrying heat from one of its ends to the other end under steady state. The variation of temperature 0 along the length x of the bar from its hot end is best described by which of the following graph options?
A)
B)
C)
D)
View Solution play_arrow
question_answer 19)
Three conducting rods of same material and cross-section are shown in figure. Temperatures of A, D and C are maintained at \[20{}^\circ C,\text{ }90{}^\circ C\] and \[0{}^\circ C\]. The ratio of lengths of BD and BC if there is no heat flow in AB is:
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 20)
The energy spectrum of a black body exhibits a maximum around a wavelength \[{{\lambda }_{0}}\]. The temperature of the black body is now changed such that the energy is maximum around a wavelength \[3{{\lambda }_{0}}/4\]. The power radiated by the black body will now increase by a factor of
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 21)
When a body cools by radiation, the rate of decrease of its temperature depends upon
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 22)
Two different metal rods of equal lengths & equal cross section area have their ends kept at the same temperatures \[{{\theta }_{1}}\And {{\theta }_{2}}.\] If \[{{K}_{1}}\And {{K}_{2}}\] be the thermal conductivities of rod, \[{{\rho }_{1}}\And {{\rho }_{2}}\] are their densities and \[{{s}_{1}},{{s}_{2}}\] are their specific heats, then the rate of flow of heat in the two rods will be same if
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 23)
A and B are two points on a uniform metal ring whose centre is C. The angle \[ACB=\theta \]. A and B are maintained at two different constant temperatures. When \[\theta ={{180}^{o}},\] the rate of total heat flow from A to B is 1.2W. When \[\theta ={{90}^{o}},\] this rate will be
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 24)
One day in a room a heater connected to supply maintained temperature \[20{}^\circ C\] when outside temperature was \[-20{}^\circ C\]. Another day with the same heater, in the same room, temperature was \[10{}^\circ C\] when outside temperature was \[-40{}^\circ C\]. If temperature of heater is same both the days. Find this value. (use \[\frac{dT}{dt}=k(T-{{T}_{0}})\] and k is same for both days).
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 25)
A rod of length i and cross section area A has a variable thermal conductivity given by \[k=\alpha T,\] where a is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperatures \[{{T}_{1}}\] and \[{{T}_{2}}({{T}_{1}}>{{T}_{2}})\]. Heat current flowing through the rod will be
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 26)
One end of a conducting rod is maintained at temperature \[50{}^\circ C\] and at the other end, ice is melting at \[0{}^\circ C\]. The rate of melting of ice is doubled if:
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 27)
Twelve conducting rods form the riders of a uniform cube of side l. If in steady state, B and H ends of the rod are at \[100{}^\circ C\] and \[0{}^\circ C\]. Find the temperature of the junction A:
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 28)
A metallic sphere having radius 0.08 m and mass m = 10 kg is heated to a temperature of \[227{}^\circ C\] and suspended inside a box whose walls are at a temperature of \[27{}^\circ C\]. The maximum rate at which its temperature will fall, is (Take \[e=1,\] Stefan's constant \[\sigma =5.8\times {{10}^{-8}}W{{m}^{-2}}{{K}^{-4}}\] and specific heat of the metal \[s=90\,cal/kg/\deg ,\,J=4.2\] joules/calorie)
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 29)
A sphere, a cube and a thin circular plate all made of the same material and having the same mass, are initially heated to a temperature of \[200{}^\circ C\]. Which of these objects will cool slowest when left in air at room temperature?
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 30)
An electric heater, assumed to be a black body has a temperature of \[727{}^\circ C\]. If its temperature is raised to \[1727{}^\circ C,\] the amount of energy radiated per unit time now as compared with that in the first case will be
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 31)
A bucket full of hot water is kept in a room and it cools from \[75{}^\circ C\] to \[70{}^\circ C~\] in \[{{T}_{1}}\] minutes, from \[70{}^\circ C\] to \[65{}^\circ C\] in \[{{T}_{2}}\] minutes and from \[65{}^\circ C\] to \[60{}^\circ C~\] in \[{{T}_{3}}\] minutes. Then
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 32)
Assuming the sun to be a spherical body of radius R at a temperature of TK, evaluate the total radiant power, incident on earth, at a distance from the sun. Where r0 is the radius of the earth and a is Stefans constant.
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 33)
Direction: Consider a spherical body A of radius R which placed concentrically in a hollow enclosure H, of radius 4R as shown in the figure. The temperature of the body A and H are \[{{T}_{A}}\] and \[{{T}_{H}},\] respectively. Emissivity, transitivity and reflectivity of two bodies A and H are \[\text{(}{{e}_{A}},\text{ }{{e}_{H}})\text{ (}{{t}_{A}},\text{ }{{t}_{H}}\text{)}\] and \[({{r}_{A}},\text{ }{{r}_{H}})\] respectively. For answering following questions assume no absorption of the thermal energy by the space in-between the body and enclosure as well as outside the enclosure and all radiations to be emitted and absorbed normal to the surface. [Take \[\sigma \times \,4\pi {{R}^{2}}\,\times \,{{300}^{4}}=\,\beta J{{s}^{-1}}\]]
The temperature of A (a perfect black body) is \[{{T}_{A}}=300K\] and temperature of H is \[{{T}_{0}}=OK\]. For H take \[{{e}_{H}}=0.5\] and \[t=0.5\]. For this situation mark out the correct statement(s).
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 34)
Direction: Consider a spherical body A of radius R which placed concentrically in a hollow enclosure H, of radius 4R as shown in the figure. The temperature of the body A and H are \[{{T}_{A}}\] and \[{{T}_{H}},\] respectively. Emissivity, transitivity and reflectivity of two bodies A and H are \[\text{(}{{e}_{A}},\text{ }{{e}_{H}})\text{ (}{{t}_{A}},\text{ }{{t}_{H}}\text{)}\] and \[({{r}_{A}},\text{ }{{r}_{H}})\] respectively. For answering following questions assume no absorption of the thermal energy by the space in-between the body and enclosure as well as outside the enclosure and all radiations to be emitted and absorbed normal to the surface. [Take \[\sigma \times \,4\pi {{R}^{2}}\,\times \,{{300}^{4}}=\,\beta J{{s}^{-1}}\]]
In above question, if body A has \[{{e}_{A}}=0.5,\] \[{{r}_{A}}=0.5\] and for H, \[{{e}_{H}}=0.5,\] \[r=0.5,\] then mark out the correct statement.
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
question_answer 35)
Direction: Consider a spherical body A of radius R which placed concentrically in a hollow enclosure H, of radius 4R as shown in the figure. The temperature of the body A and H are \[{{T}_{A}}\] and \[{{T}_{H}},\] respectively. Emissivity, transitivity and reflectivity of two bodies A and H are \[\text{(}{{e}_{A}},\text{ }{{e}_{H}})\text{ (}{{t}_{A}},\text{ }{{t}_{H}}\text{)}\] and \[({{r}_{A}},\text{ }{{r}_{H}})\] respectively. For answering following questions assume no absorption of the thermal energy by the space in-between the body and enclosure as well as outside the enclosure and all radiations to be emitted and absorbed normal to the surface. [Take \[\sigma \times \,4\pi {{R}^{2}}\,\times \,{{300}^{4}}=\,\beta J{{s}^{-1}}\]]
Consider two cases, first one in which A is a perfect black body and the second in which A is a non-black body. In both the cases, temperature of body A is same equal to 300K and H is at temperature 600K. For H, \[t=0\] and \[a\ne 1\]. For this situation, mark out the correct statement.
A)
done
clear
B)
done
clear
C)
done
clear
D)
done
clear
View Solution play_arrow
 done
clear
done
clear
 done
clear
done
clear
 done
clear
done
clear
 done
clear
done
clear
