A) \[{{V}_{A}}={{V}_{C}}\ne {{V}_{B}}\]
B) \[{{V}_{C}}={{V}_{B}}\ne {{V}_{A}}\]
C) \[{{V}_{C}}\ne {{V}_{B}}\ne {{V}_{A}}\]
D) \[{{V}_{C}}={{V}_{B}}={{V}_{A}}\]
Correct Answer: A
Solution :
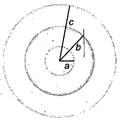
| [a] Hence, \[{{V}_{A}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\,\frac{\sigma 4\pi {{a}^{2}}}{a}-\frac{1}{4\pi {{\varepsilon }_{0}}}\,\frac{\sigma 4\pi {{b}^{2}}}{b}\] |
| \[+\frac{1}{4\,\pi {{\varepsilon }_{0}}},\,\,\frac{\sigma 4\pi {{c}^{2}}}{c}\] |
| \[=\frac{\sigma }{{{\varepsilon }_{0}}}(a-b+c)=\frac{\sigma }{{{\varepsilon }_{0}}}(2a)\,\]\[(\because \,c=a+b)\] |
 |
| \[{{V}_{B}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\,-\,\frac{\sigma 4\pi {{\alpha }^{2}}}{a}\,-\frac{1}{4\pi {{\varepsilon }_{0}}}\,\frac{\sigma 4\pi {{b}^{2}}}{b}\] |
| \[+\frac{1}{4\,\pi {{\varepsilon }_{0}}},\,\,\frac{\sigma 4\pi {{c}^{2}}}{c}\] |
| \[=\frac{\sigma }{{{\varepsilon }_{0}}}\,\left( \frac{{{a}^{2}}}{c}-b+c \right)\,=\frac{\sigma }{{{\varepsilon }_{0}}}(2a)\,\,(\because \,c=a+b)\] |
| And \[{{V}_{C}}=\frac{1}{4\pi {{\varepsilon }_{0}}}\cdot \frac{\sigma \,4\,\pi {{\sigma }^{2}}}{c}-\frac{1}{4\,\pi {{\varepsilon }_{0}}}\frac{\sigma \,4\,\pi \,{{b}^{2}}}{c}\] |
| \[+\frac{1}{4\,\pi {{\varepsilon }_{0}}},\,\,\frac{\sigma 4\pi {{c}^{2}}}{c}\] |
| \[=\frac{\sigma }{{{\varepsilon }_{0}}}\,\left( \frac{{{a}^{2}}}{c}-\frac{{{b}^{2}}}{c}+c \right)\,=\frac{\sigma }{{{\varepsilon }_{0}}}(2a)\,\,(\because \,c=a+b)\] |
| Hence, \[{{V}_{A}}={{V}_{C}}\ne {{V}_{B}}\] |
You need to login to perform this action.
You will be redirected in
3 sec
