-
question_answer1)
A massive platform of mass M is moving with speed \[v=6m{{s}^{-1}}\]. At. \[t=0,\] a body of mass \[m(m<<M)\] is gently placed on the platform. If coefficient of friction between the body and platform is \[\mu =0.3\] and \[g=10\,\,m/{{s}^{2}}\]. Then,
A)
the body covers a distance 3 m on the platform in the direction of motion of the platform done
clear
B)
the body covers a distance 3 m on the platform opposite to the direction of motion of platform before coming to rest done
clear
C)
the body covers a distance 6 m on the platform in the direction of motion of the platform done
clear
D)
the body covers a distance 6 m on the platform opposite to the direction of motion of platform before coming to rest done
clear
View Solution play_arrow
-
question_answer2)
| Two blocks are placed on a wedge with coefficients of friction being different for two blocks. Choose the correct option (friction is not sufficient to prevent the motion). |
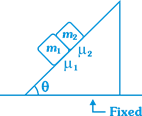 |
A)
if\[{{m}_{1}}<{{m}_{2}}\], then normal reaction between blocks will be non-zero done
clear
B)
if\[{{m}_{1}}={{m}_{2}}\]then normal reaction between the blocks will be zero done
clear
C)
if\[{{\mu }_{1}}={{\mu }_{2}}\], then normal reaction between the blocks will be zero done
clear
D)
None of the above done
clear
View Solution play_arrow
-
question_answer3)
An insect crawls up on a hemispherical surface very slowly (figure). The coefficient of friction between the insect and the surface is \[1/3\]. If the line joining the centre of hemispherical surface of the insect makes an angle a with the vertical, the maximum possible value of a is given by
A)
cot\[\alpha \] = 3 done
clear
B)
tan\[\alpha \]= 3 done
clear
C)
sec\[\alpha \]= 3 done
clear
D)
cosec\[\alpha \]= 3 done
clear
View Solution play_arrow
-
question_answer4)
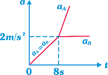
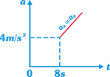
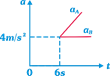
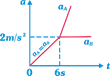
| A block of mass \[{{m}_{A}}=4\,\,kg\] is kept over another block of mass \[{{m}_{B}}=8\,kg\] which is kept on a smooth horizontal surface. The coefficient of friction between the blocks is 0.4. A time varying horizontal force \[F=4t\] is applied at \[t=0\] on 4 kg mass. Then the acceleration time graph of the masses A and B is \[(g=10\,m/{{s}^{2}})\] |
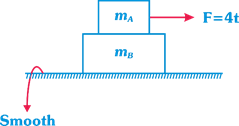 |
A)
B)
C)
D)
View Solution play_arrow
-
question_answer5)
| Let \[\frac{1}{2\sqrt{3}}\sec \] be the coefficient of friction between blocks of mass m and M. The pulleys are frictionless and strings are massless. Acceleration of mass m is |
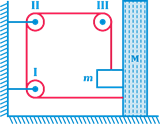 |
A)
\[\frac{\sqrt{5}\,mg}{M+\sqrt{5}\,m\,+2\,\mu \,m}\] done
clear
B)
\[\frac{2\,mg}{m+5\,M\,+2\,\mu \,m}\] done
clear
C)
\[\frac{2\sqrt{5}\,mg}{M+5\,M\,+2\,\mu \,m}\] done
clear
D)
\[\frac{5\sqrt{2}\,mg}{M+\sqrt{5}\,m\,+\sqrt{2}\,\mu \,m}\] done
clear
View Solution play_arrow
-
question_answer6)
A heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25 then the maximum fraction of length of chain that can hang over on edge of table is
A)
20% done
clear
B)
35% done
clear
C)
25% done
clear
D)
15% done
clear
View Solution play_arrow
-
question_answer7)
The time taken by a body in sliding down a rough inclined plane of angle of inclination \[45{}^\circ \] is n times the time taken by the same body in slipping down a similar frictionless plane. The coefficient of dynamic friction between the body and the plane will be
A)
\[1/(1-{{n}^{2}})\] done
clear
B)
\[1-(1/{{n}^{2}})\] done
clear
C)
Ö\[\left\{ 1-(1/{{n}^{2}}) \right\}\] done
clear
D)
Ö\[\left\{ 1/(1-{{n}^{2}}) \right\}\] done
clear
View Solution play_arrow
-
question_answer8)
| The masses of the blocks A and B are 0.5 kg and 1 kg respectively. These are arranged as shown in the figure and are connected by a massless string. The coefficient of friction between all contact surfaces is 0.4. The force, necessary to move the block B with constant velocity, will be \[(g=10\,m/{{s}^{2}})\] |
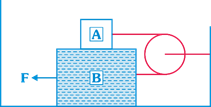 |
A)
5 N done
clear
B)
10 N done
clear
C)
15 N done
clear
D)
20 N done
clear
View Solution play_arrow
-
question_answer9)
| A horizontal force of 10 N is necessary to just hold a block stationary against a wall. The coefficient or friction between the block and the wall is 0.2. The weight of the block is : \[\left( g=10\text{ }m/{{s}^{2}} \right)\] |
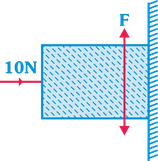 |
A)
20 N done
clear
B)
50 N done
clear
C)
100 N done
clear
D)
2 N done
clear
View Solution play_arrow
-
question_answer10)
| If the coefficient of friction between A and B is \[{{m}_{2}}\], the maximum horizontal acceleration of the wedge A for which B will remain at rest with respect to the wedge is: |
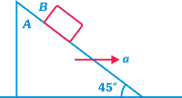 |
A)
\[{{m}_{1}}={{m}_{2}}\] done
clear
B)
\[{{m}_{2}}\] done
clear
C)
\[{{m}_{1}}={{m}_{2}}\] done
clear
D)
\[{{m}_{2}}\] done
clear
View Solution play_arrow
-
question_answer11)
| A bead of mass m is located on a parabolic wire with its axis vertical and vertex directed towards downward as in figure and whose equation is\[{{x}^{2}}=ay\]. If the coefficient of friction is \[{{M}_{1}}\] the highest distance above the x-axis at which the particle will be in equilibrium is |
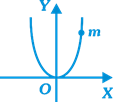 |
A)
\[\mu a\] done
clear
B)
\[{{\mu }^{2}}a\] done
clear
C)
\[\frac{1}{4}{{\mu }^{2}}a\] done
clear
D)
\[\frac{1}{2}\mu a\] done
clear
View Solution play_arrow
-
question_answer12)
A weight w is to be moved from the bottom to the top of an inclined plane of inclination 9 to the horizontal. If a smaller force is to be applied to drag it along the plane in comparison to lift it vertically up, the coefficient of friction should be such that:
A)
\[\mu >\tan \left( \frac{\pi }{4}-\frac{\theta }{2} \right)\] done
clear
B)
\[\mu <\tan \left( \frac{\pi }{4}-\frac{\theta }{2} \right)\] done
clear
C)
\[\mu <\tan \theta \] done
clear
D)
\[\mu >\tan \frac{\pi }{4}\] done
clear
View Solution play_arrow
-
question_answer13)
| A block is given velocity 10 m/s along the fixed inclined as shown in figure from the bottom of the inclined plane. Find the total distance travelled along the inclined plane, if the coefficient of friction is equal to 0.5: |
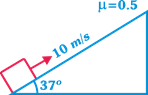 |
A)
5m done
clear
B)
10m done
clear
C)
\[\frac{25}{3}m\] done
clear
D)
\[\frac{50}{3}m\] done
clear
View Solution play_arrow
-
question_answer14)
What is the minimum stopping distance for a vehicle of mass m moving with speed v along a level road. If the coefficient of friction between the tyres and the road is \[x=40\,cm\]
A)
\[\frac{{{v}^{2}}}{2\mu g}\] done
clear
B)
\[\frac{2{{v}^{2}}}{\mu g}\] done
clear
C)
\[\frac{{{v}^{2}}}{\mu g}\] done
clear
D)
none of these done
clear
View Solution play_arrow
-
question_answer15)
| A block of mass 10 kg is kept on the fixed incline having coefficient of friction 0.8. Find the force of friction exerted on the block by inclined: |
 |
A)
100 N done
clear
B)
64 N done
clear
C)
80 N done
clear
D)
60 N done
clear
View Solution play_arrow
-
question_answer16)
| A block of mass 15 kg is resting on a rough inclined plane as shown in figure. The block is tied up by a horizontal string which has a tension of 50 N. The coefficient of friction between the surfaces of contact is \[\left( g=10\text{ }m/{{s}^{2}} \right)\] |
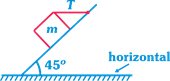 |
A)
1/2 done
clear
B)
2/3 done
clear
C)
3/4 done
clear
D)
1/4 done
clear
View Solution play_arrow
-
question_answer17)
| Car is accelerating with acceleration = 20 m/s2. A box of mass m = 10 kg that is placed inside the car it is put in contact with the vertical wall of car as shown. The friction coefficient between the box and the wall is \[\mu =0.6\]. |
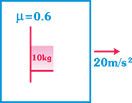 |
A)
The acceleration of the box will be \[10\,m/{{\sec }^{2}}\] done
clear
B)
The friction force acting on the box will be 100 N done
clear
C)
The contact force between the vertical wall and the box will be 100 N done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer18)
| With reference to the figure shown, if the coefficient of friction at the surfaces is 0.42, then the force F required to pull out the 6.0 kg block with an acceleration of 1.50 \[m\text{/}{{s}^{2}}\] will be: |
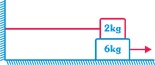 |
A)
36 N done
clear
B)
24 N done
clear
C)
84 N done
clear
D)
51 N done
clear
View Solution play_arrow
-
question_answer19)
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of friction between the block and the surface is 0.4. if the acceleration of the truck is 5 \[m\text{/}{{s}^{2}}\]. Find the frictional force acting on the block?
A)
2 N done
clear
B)
55 M done
clear
C)
4 N done
clear
D)
10 N done
clear
View Solution play_arrow
-
question_answer20)
| A block of mass m is attached with massless spring of force constant k. The block is placed over a fixed rough inclined surface for which the coefficient of friction is \[\mu =3/4.\] The block of mass m is initially at rest. The block of mass M is released from rest with spring in unstretched state. The minimum value of M required to move the block up the plane is (neglect mass of string and pulley and friction in pulley.) |
 |
A)
\[\frac{3}{5}m\] done
clear
B)
\[\frac{4}{5}m\] done
clear
C)
\[\frac{6}{5}m\] done
clear
D)
\[\frac{3}{2}m\] done
clear
View Solution play_arrow
-
question_answer21)
| Two masses A and B of 10 kg and 5 kg are connected with a string passing over a frictionless pulley fixed at the corner of a table (as shown in figure). The coefficient of friction between the table and block is 0.2. The minimum mass of C that maybe placed on A to prevent it from moving is equal to |
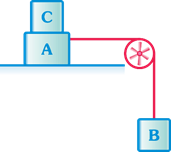 |
A)
15 kg done
clear
B)
10 kg done
clear
C)
5 kg done
clear
D)
zero done
clear
View Solution play_arrow
-
question_answer22)
If dimensions of velocity is \[b{{c}^{-1}},\] acceleration \[b{{c}^{-2}}\] and length \[ab,\] the dimensions of coefficient of friction are
A)
\[{{a}^{0}}{{b}^{0}}{{c}^{0}}\] done
clear
B)
\[{{a}^{-1}}{{b}^{0}}{{c}^{0}}\] done
clear
C)
\[{{a}^{1}}{{b}^{0}}{{c}^{0}}\] done
clear
D)
\[{{a}^{-1}}{{b}^{-1}}{{c}^{0}}\] done
clear
View Solution play_arrow
-
question_answer23)
A fireman of mass 60 kg slides down a pole. He is pressing the pole with a force of 600 N. The coefficient of friction between the hands and the pole is 0.5. With what acceleration will the fireman slide down
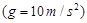
?
A)
\[1\,\,m/{{s}^{2}}\] done
clear
B)
\[2.5\,\,m/{{s}^{2}}\] done
clear
C)
\[10\,\,m/{{s}^{2}}\] done
clear
D)
\[5\,\,m/{{s}^{2}}\] done
clear
View Solution play_arrow
-
question_answer24)
| A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force\[P\]and another force Q is inclined at an angle\[\theta \]to the vertical. The block will remain in equilibrium, if the coefficient of friction between it and the surface is |
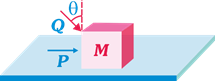 |
A)
\[\frac{(P+Q\,\sin \theta )}{(mg+Q\cos \theta )}\] done
clear
B)
\[\frac{(P\cos \theta +Q)}{(mg-Q\sin \theta )}\] done
clear
C)
\[\frac{(P+Q\cos \theta )}{(mg+Q\sin \theta )}\] done
clear
D)
\[\frac{(P\sin \theta -Q)}{(mg-Q\cos \theta )}\] done
clear
View Solution play_arrow
-
question_answer25)
| String is massless and pulley is smooth in the adjoining figure total mass or left hand side of the pulley side of the pulley is \[{{m}_{1}}\] and on right hand side is \[{{m}_{2}}\] . Friction coefficient between block B and the wedge is \[\mu =\frac{1}{2}\] and \[\theta =30{}^\circ \] Select the wrong answer |
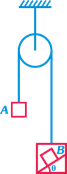 |
A)
Block B will slide down if \[{{m}_{1}}={{m}_{2}}\] done
clear
B)
Block B may remain stationary with respect to wedge, for suitable values of \[{{m}_{1}}\] and \[{{m}_{2}}\] with \[{{m}_{1}}>{{m}_{2}}\] done
clear
C)
Block B cannot remain stationary with respect to wedge in any case done
clear
D)
Block B will slide down if \[{{m}_{1}}>{{m}_{2}}\] done
clear
View Solution play_arrow
-
question_answer26)
| Mass of block A is 10 kg. Coefficient of friction between the block A and surface is 0.3. What is the maximum values of M for which system remains in equilibrium \[\left( g=10m/{{s}^{2}} \right)\] |
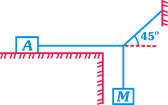 |
A)
2 kg done
clear
B)
6 kg done
clear
C)
3 kg done
clear
D)
5 kg done
clear
View Solution play_arrow
-
question_answer27)
| A particle is projected on a rough horizontal ground along positive x-axis from x = 0, with an initial speed of \[{{\text{V}}_{\text{0}}}\] The friction coefficient to the ground varies with x as Here K is a positive constant. The particle comes to rest at x equal |
 |
A)
\[\frac{{{\text{v}}_{\text{0}}}}{\sqrt{\text{Kg}}}\] done
clear
B)
\[\frac{\text{2}{{\text{v}}_{\text{0}}}}{Kg}\] done
clear
C)
\[\frac{{{\text{v}}_{\text{0}}}}{\sqrt{2Kg}}\] done
clear
D)
\[\frac{\text{2}{{\text{v}}_{\text{0}}}}{\sqrt{Kg}}\] done
clear
View Solution play_arrow
-
question_answer28)
| The member OA rotates about a horizontal axis through O with a constant counter clockwise velocity \[\omega =3\] \[\text{rad}/\text{sec}\]. As it passes the position\[\theta ={{0}^{o}}\], a small mass m is placed upon it at a radial distance r = 0.5 m. If the mass is observed to slip at \[\theta ={{37}^{o}}\], the coefficient of friction between the mass & the member is: |
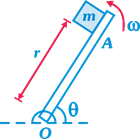 |
A)
\[\frac{3}{16}\] done
clear
B)
\[\frac{9}{16}\] done
clear
C)
\[\frac{4}{9}\] done
clear
D)
\[\frac{5}{9}\] done
clear
View Solution play_arrow
-
question_answer29)
| Two blocks (m and M) are arranged as shown in Fig. 21. If there is friction between ground and M only and other surfaces are frictionless. The coefficient of friction between ground and M is \[\mu =0.75\] . The maximum ratio of m and M (m/M) so that the system remains at rest is |
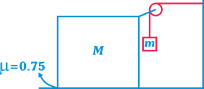 |
A)
\[1/4\] done
clear
B)
3 done
clear
C)
\[1/3\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer30)
A block A is kept on a block B. Friction between B and ground is negligible. \[{{\mu }_{s}}\] and \[{{\mu }_{K}}\] are the coefficients of static and kinetic friction between A and B, respectively. A horizontal force F is applied on A. \[{{a}_{1}}\] is the acceleration of B just before A slips on B and \[{{a}_{2}}\] is the acceleration of B after A slips on B. Assume \[{{\mu }_{s}}>{{\mu }_{K}}\]. Then
A)
\[{{a}_{1}}>{{a}_{2}}\] done
clear
B)
\[{{a}_{1}}<{{a}_{2}}\] done
clear
C)
\[{{a}_{1}}={{a}_{2}}\] done
clear
D)
None of these done
clear
View Solution play_arrow
-
question_answer31)
A boy of mass m is sliding down a vertical pole by pressing it with a horizontal force F. If \[\mu \]is the coefficient of friction between his palms and the pole, the acceleration with which he slides down is
A)
\[g\] done
clear
B)
\[\frac{\mu F}{m}\] done
clear
C)
\[g+\frac{\mu F}{m}\] done
clear
D)
\[g-\frac{\mu F}{m}\] done
clear
View Solution play_arrow
-
question_answer32)
| A 40 kg slab rests on a frictionless floor as shown in the figure. A 10 kg block rests on the top of the slab. The static coefficient of friction between the block and slab is 0.60 while the kinetic friction is 0.40. The 10 kg block is acted upon by a horizontal force 100 N. If \[g=9.8\,m/{{s}^{2}},\]the resulting acceleration of the slab will be |
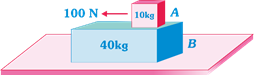 |
A)
\[1\,m/{{s}^{2}}\] done
clear
B)
\[1.5\,m/{{s}^{2}}\] done
clear
C)
\[2\,m/{{s}^{2}}\] done
clear
D)
\[6\,m/{{s}^{2}}\] done
clear
View Solution play_arrow
-
question_answer33)
| A cart of mass M has a block of mass m attached to it as shown in fig. The coefficient of friction between the block and the cart is u. What is the minimum acceleration of the cart so that the block m does not fall? |
 |
A)
\[\mu g\] done
clear
B)
\[g/\mu \] done
clear
C)
\[\mu /g\] done
clear
D)
\[M\mu g\text{/}m\] done
clear
View Solution play_arrow
-
question_answer34)
| In the arrangement shown in the figure. The mass of wedge A and that of the block B are 3m and in respectively. Friction exists between A and B only. The mass of the block C is m. |
| The force F = 19.5 m x g is applied on the block C as shown in the figure. The minimum coefficient of friction (\[\mu \]) between A and B so that B remains stationary with respect to wedge A will be |
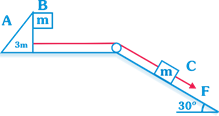 |
A)
\[\frac{2}{3}\] done
clear
B)
\[\frac{1}{10}\] done
clear
C)
\[\frac{2}{5}\] done
clear
D)
\[\frac{1}{4}\] done
clear
View Solution play_arrow
-
question_answer35)
| A worker piles up sand onto a circular area of radius R. No sand is to spill onto the surrounding area. The coefficient of friction of sand on sand is \[\mu \]. The greatest volume of the sand that can be stored in the manner is |
 |
A)
\[\frac{\pi \mu {{R}^{3}}}{3}\] done
clear
B)
\[\frac{\pi \mu {{R}^{3}}}{6}\] done
clear
C)
\[\frac{\pi {{R}^{3}}}{3\mu }\] done
clear
D)
None done
clear
View Solution play_arrow
 done
clear
done
clear
 done
clear
done
clear
 done
clear
done
clear
 done
clear
done
clear
