2. Questions Bank
  3. JEE Main & Advanced
  4. Mathematics
  5. Linear Programming

JEE Main & Advanced Mathematics Linear Programming Question Bank Critical Thinking

  • question_answer
    In equations \[3x-y\ge 3\] and \[4x-y>4\] [MP PET 2001]

    A) Have solution for positive x and y            

    B) Have no solution for positive x and y

    C) Have solution for all x

    D) Have solution for all y

    Correct Answer: A

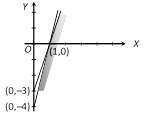
    Solution :

    • Following figure will be obtained on drawing the graphs of given in equations.                   
    • From \[3x-y\ge 3,\frac{x}{1}+\frac{y}{-3}=1\]                   
    • From \[4x-y>4,\,\frac{x}{1}+\frac{y}{-4}=1\]                                
    • Clearly the common region of both is true for positive value of (x, y). It is also true for positive value of x and negative value of y.


You need to login to perform this action.
You will be redirected in 3 sec spinner