question_answer

Direction: Q.41 to Q.45

When a rectangular loop PQRS of sides 'a' and 'b’ carrying current I is placed in uniform magnetic

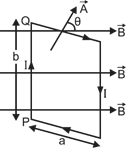field \[\overrightarrow{B}\], such that area vector \[\overrightarrow{A}\] makes an angle \[\theta \] with direction of magnetic field, then forces on the arms QR and SP of loop are equal,          opposite and collinear, thereby perfectly cancel each other, whereas forces on the arms PQ and RS of loop are equal and opposite but not collinear, so they give rise to torque on the loop.

Force on side PQ or RS of loop is \[F=lbB\,\sin \,90{}^\circ =lbB\] and perpendicular distance between two non-collinear forces is \[{{r}_{\bot }}=a\,\sin \,\theta \]

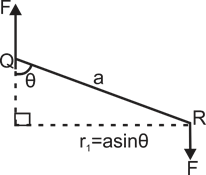So, torque on the loop, \[\tau =JAB\,\sin \theta \]

In vector form, torque \[\tau =\overrightarrow{M}\times \overrightarrow{B}\]

where \[\overrightarrow{M}\times NI\,\overrightarrow{A}\] is called magnetic dipole moment of current loop and is directed in direction of area vector \[\overrightarrow{A}\] i.e., normal to the plane of loop.

Read the given passage carefully and give the answer of the following questions.

                                A circular loop of area \[1\text{ }c{{m}^{2}}\], carrying a current of 10 A is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is:

A) zero

B)                                     \[{{10}^{-4}}Nm\]

C)             \[~{{10}^{-2}}Nm\]               

D)             1 N m