question_answer

Direction: Q.26 to Q.30

Ampere's law gives a method to calculate the magnetic field due   to   given   current     distribution. According to it, the circulation \[\oint{\overrightarrow{B}\cdot d\,\overrightarrow{l}}\] of the resultant magnetic field along a

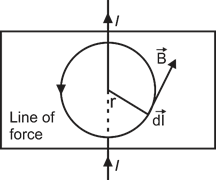closed plane curve is equal to \[{{\mu }_{0}}\] times the total current crossing the area bounded by the closed curve provided the electric field inside the loop remains constant. Ampere's law is more useful under certain symmetrical conditions. Consider one such case of a long straight wire with circular cross-section (radius R) carrying current I uniformly distributed across this cross-section.

Read the given passage carefully and give the answer of the following questions.

The magnetic field at a radial distance r from the centre of the wire in the region r > R, is:

A)             \[\frac{{{\mu }_{0}}l}{2\pi r}\]                                  

B) \[\frac{{{\mu }_{0}}l}{2\pi R}\]

C)             \[\frac{{{\mu }_{0}}l{{R}^{2}}}{2\pi r}\]        

D)             \[\frac{{{\mu }_{0}}l{{r}^{2}}}{2\pi R}\]