| Direction: Q.21 to Q.25 |
| The electrical capacitance of a conductor is the measure of its ability to hold electric charge. An isolated spherical conductor of radius R. The charge Q is uniformly distributed over its entire surface. It can be assumed to be concentrated at the centre of the sphere. The potential at any point on the surface of the spherical conductor will be |
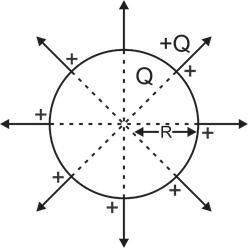 |
| \[V=\frac{1}{4\pi {{\varepsilon }_{0}}}\frac{Q}{R}\]. |
| Capacitance of the spherical conductor situated in vacuum is |
| \[C=\frac{Q}{V}=\frac{Q}{\frac{1}{4\pi {{\varepsilon }_{0}}}.\frac{Q}{R}}\] or \[C=4\pi {{\varepsilon }_{0}}R\] |
| Clearly, the capacitance of a spherical conductor is proportional to its radius. |
| The radius of the spherical conductor is 1 F capacitance is \[R=\frac{1}{4\pi {{\varepsilon }_{0}}}.C\]and this radius is about 1500 times the radius of earth\[\left( \tilde{\ }6\times {{10}^{3}}\,km \right)\]. |
| Read the given passage carefully and give the answer of the following questions. |
A) 90 cm
B) 45 cm
C) 45 m
D) 90 m
Correct Answer: B
Solution :
(b) 45 cm Here, \[C=50pF=50\times {{10}^{-12}}F,\,V={{10}^{4}}V\] \[R=\frac{1}{4\pi {{\varepsilon }_{0}}}.C=9\times {{10}^{9}}m{{F}^{-1}}\times 50\times {{10}^{-12}}F\] \[=45\times {{10}^{-2}}m=45\,cm\]You need to login to perform this action.
You will be redirected in
3 sec
