9th Class Mathematics Coordinate Geometry Question Bank

done Coordinate Geometry Total Questions - 25

• question_answer1)
  The linear equation \[y=2x+3\]cuts the y-axis at ____.
  A)
   (0, 3)                            done clear
  B)
   (0, 2)    done clear
  C)
  \[\left( \frac{3}{2},0 \right)\]        done clear
  D)
         \[\left( \frac{2}{3},0 \right)\]        done clear
  View Solution play_arrow

• question_answer2)
  (2, 1) is a point, which belongs to the line____.
  A)
  \[x=y\]              done clear
  B)
         \[~y=x+1\]       done clear
  C)
  \[~2y=x\]        done clear
  D)
         \[~xy=1\]         done clear
  View Solution play_arrow

• question_answer3)
  One set of ordered pair which belongs to a straight line represented by an equation \[y=2x-1\]is____.
  A)
   (1, 1)                done clear
  B)
          (2, 1) done clear
  C)
   (1, 2)                done clear
  D)
          (3, 1) done clear
  View Solution play_arrow

• question_answer4)
  The axis on which the point (0, - 4) lie, is
  A)
   Positive x-axis done clear
  B)
   Negative x-axis done clear
  C)
   Positive y-axis done clear
  D)
   Negative y-axis done clear
  View Solution play_arrow

• question_answer5)
  The coordinate axes divide the plane into
  A)
   One part                       done clear
  B)
   Two parts         done clear
  C)
   Three parts        done clear
  D)
          Four parts         done clear
  View Solution play_arrow

• question_answer6)
  If \[(x+3,5)=(2,\,2-y)\] then the values of the \[x\] and  y respectively are
  A)
   5, 3                              done clear
  B)
   -1, -3    done clear
  C)
   0, -3                 done clear
  D)
          1, 3                  done clear
  View Solution play_arrow

• question_answer7)
  The value of \['x'\] in the ordered pair \[(x,-8)\] if the ordinate of the pair is 4 more than the abscissa is ___.
  A)
   -4                                done clear
  B)
   -8                    done clear
  C)
   -12                   done clear
  D)
          4         done clear
  View Solution play_arrow

• question_answer8)
  The point (-5, 6) lies in
  A)
   \[{{I}^{st}}\]quadrant              done clear
  B)
  \[I{{I}^{nd}}\] quadrant           done clear
  C)
  \[II{{I}^{rd}}\] quadrant           done clear
  D)
         \[I{{V}^{th}}\] quadrant           done clear
  View Solution play_arrow

• question_answer9)
  The point at which the two coordinate axes meet is called ____.
  A)
   Abscissa                       done clear
  B)
   Ordinate           done clear
  C)
   Origin               done clear
  D)
          Quadrant          done clear
  View Solution play_arrow

• question_answer10)
  The coordinates of two points are A(3, 4) and B(-2, 5), then (abscissa of A) - (abscissa of B) is____.
  A)
   1                                 done clear
  B)
   -1                    done clear
  C)
   5                     done clear
  D)
          -5 done clear
  View Solution play_arrow

• question_answer11)
  The signs of abscissa and ordinate of a point in quadrant II are respectively____.
  A)
  \[(+,-)\]                         done clear
  B)
  \[(-,+)\] done clear
  C)
  \[(-,-)\]               done clear
  D)
         \[(+,+)\]    done clear
  View Solution play_arrow

• question_answer12)
  Two points having same abscissa but different ordinates lie on ____.
  A)
  \[x-\]axis done clear
  B)
  \[y-\]axis done clear
  C)
   A line parallel to y-axis done clear
  D)
   A line parallel to\[x-\]axis done clear
  View Solution play_arrow

• question_answer13)

  DIRECTION: Study the graph and answer the following questions.

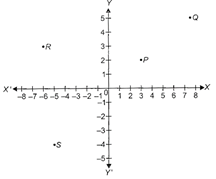  The coordinate of point S are ____.
  A)
   (4, 5)                            done clear
  B)
   (-5,-4)   done clear
  C)
                      (-4,-5)               done clear
  D)
          (5, 4)    done clear
  View Solution play_arrow

• question_answer14)

  DIRECTION: Study the graph and answer the following questions.

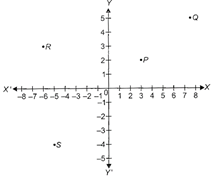  Sum of abscissae of point P and R is
  A)
   5                     done clear
  B)
          6         done clear
  C)
   9                     done clear
  D)
          -3                    done clear
  View Solution play_arrow

• question_answer15)

  DIRECTION: Study the graph and answer the following questions.

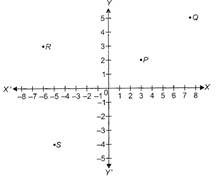  The point whose abscissae is 2 more than the ordinate is ____.
  A)
   P                                 done clear
  B)
   R                     done clear
  C)
   O                     done clear
  D)
          S                     done clear
  View Solution play_arrow

• question_answer16)

  DIRECTION: Study the graph and answer the following questions.

  The difference between ordinates of R and Q is ____.
  A)
   8                                 done clear
  B)
   3                     done clear
  C)
   2                     done clear
  D)
          14        done clear
  View Solution play_arrow

• question_answer17)
  The area of the triangle formed by the points P (0, 1), 0 (0, 5) and R (3, 4) is
  A)
   16 sq. units                   done clear
  B)
   8 sq. units         done clear
  C)
   4 sq. units         done clear
  D)
          6 sq. units                     done clear
  View Solution play_arrow

• question_answer18)
  The perpendicular distance of the point (-7, 8) from the \[x-\]axis is ____.
  A)
   7                                 done clear
  B)
   8                     done clear
  C)
   -7                    done clear
  D)
          1         done clear
  View Solution play_arrow

• question_answer19)
  The point (3, 0) lies ____.
  A)
   On \[x-\]axis     done clear
  B)
   On y-axis          done clear
  C)
   In I quadrant     done clear
  D)
          None of these                done clear
  View Solution play_arrow

• question_answer20)
  The signs of the abscissa and ordinate of a point in the fourth quadrant respectively are___.
  A)
   +, +                            done clear
  B)
   -, -                   done clear
  C)
   +, -                 done clear
  D)
          -, + done clear
  View Solution play_arrow

• question_answer21)
  State T' for true and 'F' for false.

  (i) Origin is the only point which lies on both the axes.

  (ii) The point (2, -2) and point (-2, 2) lies in the same quadrant.

  (iii) A point lies on y-axis at a distance 2 units from x-axis then it's coordinates are (2, 0).

  (iv) Abscissa of a point is positive in I quadrant and also in II quadrant.

  A)

  (i)	(ii)	(iii)	(iv)
  F	T	F	T

                  done clear
  B)

  (i)	(ii)	(iii)	(iv)
  T	F	F	F

                  done clear
  C)

  (i)	(ii)	(iii)	(iv)
  F	T	T	F

                  done clear
  D)

  (i)	(ii)	(iii)	(iv)
  T	F	T	F

  done clear
  View Solution play_arrow

• question_answer22)
  Fill in the blanks.

  (i) Point B is 3 spaces right and one space above from the point\[A(-1,-2).\]So point B lies in quadrant P.

  (ii) Point B is 40 spaces left and 0.02 spaces above from the point A (20, 0.18). So point B lies in quadrant Q.

  (iii) Point B is 15 spaces right and 15 spaces below from the point A (-15,0). So, coordinate of point B are R.

  (iv) A man moves 30 metres towards Northand then moves 50 metres towards South and finally 10 metres towards East. Considering his initial position at origin, the coordinate of his final destination are S.

  A)

  P	Q	R	S
  II	I	(0,15)	(-10,20)

                  done clear
  B)

  P	Q	R	S
  IV	II	(0.-15)	(10,-20)

                  done clear
  C)

  P	Q	R	S
  II	IV	(10,-20)	(0,-15)

                  done clear
  D)

  P	Q	R	S
  I	II	(0,15)	(10,20)

  done clear
  View Solution play_arrow

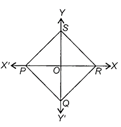
• question_answer23)
  In the given figure, PQRS is a rhombus whose diagonal PR and QS are along coordinate axis and PR = 12 units and QS = 6 units. Now, if T is a point which is 5 spaces right and 2 spaces above S. Find:

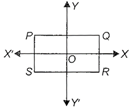
  (i) sum of abscissae of P and T.

  (ii) sum of ordinates of Q, R and T.

  A)

  (i)	(ii)
  -1	2

                  done clear
  B)

  (i)	(ii)
  1	-2

                  done clear
  C)

  (i)	(ii)
  1	2

                  done clear
  D)

  (i)	(ii)
  -1	-2

  done clear
  View Solution play_arrow

• question_answer24)
  In the given figure, PQRS is a rectangle with its centre at origin and length PQ = 2a units and breadth QR = 2b units. Find coordinates of all of its vertices.
  A)
   P(a, - b), Q(a, b), R(-a, b), S(-a, -b) done clear
  B)
   P(a, - b), Q(a, b), R(a, - b), S(-a, -b) done clear
  C)
   P(-a, b), Q(a, b), R(a, - b), S (-a, - b) done clear
  D)
   P(-a, b), Q(a, 6), R(a, - b), S(-a, b) done clear
  View Solution play_arrow

• question_answer25)
  Match the following.

  Column-I	Column-II
  (P) The  area  of \[\Delta OAB\](i)  with  O(0,  0),A{4,  0)  and B (0,  8) is	14 sq. units
  (Q) The area  of \[\Delta ABC\](ii)  with A (2,  0), 6(6,  0) and C (4, 6) is	16 sq. units
  (R) The area of \[\Delta OAB\](iii) with O(0, 0),A(7, 0) and B (0,4) is	12 sq. units

           
  A)
   \[(P)\to (iii),(Q)\to (i),(R)\to (iii)\] done clear
  B)
   \[(P)\to (iii),(Q)\to (i),(R)\to (ii)\] done clear
  C)
   \[(P)\to (iii),(Q)\to (ii),(R)\to (i)\] done clear
  D)
   \[(P)\to (ii),(Q)\to (iii),(R)\to (i)\] done clear
  View Solution play_arrow