Molecular Speeds Or Velocities
Category : JEE Main & Advanced
(1) At any particular time, in the given sample of gas all the molecules do not possess same speed, due to the frequent molecular collisions with the walls of the container and also with one another, the molecules move with ever changing speeds and also with ever changing direction of motion.
(2) According to Maxwell, at a particular temperature the distribution of speeds remains constant and this distribution is referred to as the Maxwell-Boltzmann distribution and given by the following expression,
\[\frac{d{{n}_{0}}}{n}=4\pi {{\left( \frac{M}{2\pi RT} \right)}^{3/2}}.{{e}^{-M{{u}^{2}}/2RT}}.{{u}^{2}}dc\]
where, \[d{{n}_{0}}=\] Number of molecules out of total number of molecules n, having velocities between c and \[c+dc\], \[d{{n}_{0}}/n=\]Fraction of the total number of molecules, M = molecular weight, T = absolute temperature. The exponential factor \[{{e}^{-M{{u}^{2}}/2RT}}\] is called Boltzmann factor.
(3) Maxwell gave distribution curves of molecular speeds for \[C{{O}_{2}}\] at different temperatures. Special features of the curve are :
(i) Fraction of molecules with two high or two low speeds is very small.
(ii) No molecules has zero velocity.
(iii) Initially the fraction of molecules increases in velocity till the peak of the curve which pertains to most probable velocity and thereafter it falls with increase in velocity.
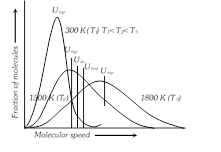
(4) Types of molecular speeds or Velocities
(i) Root mean square velocity \[({{u}_{rms}})\] : It is the square root of the mean of the squares of the velocity of a large number of molecules of the same gas.
\[{{u}_{rms}}=\sqrt{\frac{u_{1}^{2}+u_{2}^{2}+u_{3}^{2}+.....u_{n}^{2}}{n}}\]
\[{{u}_{rms}}=\sqrt{\frac{3PV}{(m{{N}_{0}})=M}}=\sqrt{\frac{3RT}{(m{{N}_{0}})=M}}\]\[=\sqrt{\frac{3RT}{M}}=\sqrt{\frac{3kT}{m}}=\sqrt{\frac{3P}{d}}\]
where k = Boltzmann constant \[=\frac{R}{{{N}_{0}}}\]
(a) For the same gas at two different temperatures, the ratio of RMS velocities will be, \[\frac{{{u}_{1}}}{{{u}_{2}}}=\sqrt{\frac{{{T}_{1}}}{{{T}_{2}}}}\]
(b) For two different gases at the same temperature, the ratio of RMS velocities will be, \[\frac{{{u}_{1}}}{{{u}_{2}}}=\sqrt{\frac{{{M}_{2}}}{{{M}_{1}}}}\]
(c) RMS velocity at any temperature \[{{t}^{o}}C\] may be related to its value at S.T.P. as, \[{{u}_{t}}=\sqrt{\frac{3P(273+t)}{273d}}\].
(ii) Average velocity \[({{v}_{av}})\] : It is the average of the various velocities possessed by the molecules.
\[{{v}_{av}}=\frac{{{v}_{1}}+{{v}_{2}}+{{v}_{3}}+......{{v}_{n}}}{n}\]; \[{{v}_{av}}=\sqrt{\frac{8RT}{\pi M}}=\sqrt{\frac{8kT}{\pi m}}\]
(iii) Most probable velocity \[({{\alpha }_{mp}})\]: It is the velocity possessed by maximum number of molecules of a gas at a given temperature.
\[{{\alpha }_{mp}}=\sqrt{\frac{2RT}{M}}=\sqrt{\frac{2PV}{M}}=\sqrt{\frac{2P}{d}}\]
(5) Relation between molecular speeds or velocities,
(i) Relation between \[{{u}_{rms}}\] and \[{{v}_{av}}\]: \[{{v}_{av}}=0.9213\times {{u}_{rms}}\] or \[{{u}_{rms}}=1.085\times {{v}_{av}}\]
(ii) Relation between \[{{\alpha }_{mp}}\] and \[{{u}_{rms}}\]: \[{{\alpha }_{mp}}=0.816\times {{u}_{rms}}\] or \[{{u}_{rms}}=1.224\times {{\alpha }_{mp}}\]
(iii) Relation between \[{{\alpha }_{mp}}\] and \[{{v}_{av}}\]: \[{{v}_{av}}=1.128\times {{\alpha }_{mp}}\]
(iv) Relation between \[{{\alpha }_{mp}}\], \[{{v}_{av}}\] and \[{{u}_{rms}}\]
\[{{\alpha }_{mp}}\] : \[{{v}_{av}}\] : \[{{u}_{rms}}\]
\[\sqrt{\frac{2RT}{M}}\] : \[\sqrt{\frac{8RT}{\pi M}}\] : \[\sqrt{\frac{3RT}{M}}\]
\[\sqrt{2}\] : \[\sqrt{\frac{8}{\pi }}\] : \[\sqrt{3}\]
1.414 : 1.595 : 1.732
1 : 1.128 : 1.224
i.e., \[{{\alpha }_{mp}}<{{v}_{av}}<{{u}_{rms}}\]
You need to login to perform this action.
You will be redirected in
3 sec
