11th Class Mathematics Straight Line Notes - Mathematics Olympiads - Pair Sraight Line

 

                                                                                   Pair and Straight Line

 

Key Points to Remember

 

A hemogenous of equation of second degree of the form \[a{{x}^{2}}+2hxy+b{{y}^{2}}=0\] represents the pair of straight lines which passes through the origin.

 

(a)        If the lines are real and distinct then

\[{{h}^{2}}>ab\]

 

(b)        If the lines are real and coincidents if

\[{{h}^{2}}=ab.\]

 

(c)        If the lines are imaginary then \[{{h}^{2}}<ab.\]

Let \[y={{m}_{1}}x\to (1)\] and \[y={{m}_{2}}x\to (2)\] are two lines which are passing through the origin.

Then \[(y-{{m}_{1}}x)(y-{{m}_{2}}x)\equiv a{{x}^{2}}+2hxy+b{{y}^{2}}\]

 

\[{{y}^{2}}-({{m}_{1}}+{{m}_{2}})xy+{{m}_{1}}{{m}_{2}}{{x}^{2}}={{y}^{2}}+\frac{2h}{b}xy+\frac{a}{b}{{x}^{2}}\]

 

Equation the coefficient of same variable of the\[\frac{2h}{b}=({{m}_{1}}+{{m}_{2}})\]we have, \[({{m}_{1}}+{{m}_{2}})=\frac{2h}{b}\] & \[{{m}_{1}}.{{m}_{2}}=\frac{a}{b}\]

• Angle between the pair of straight lines

Let q be the angle between the two given pair of straight line \[a{{x}^{2}}+2hxy+b{{y}^{2}}=0,\] which are passing through origin is written as

            \[\tan \theta =\pm \frac{2\sqrt{{{h}^{2}}}-ab}{a+b}\]

for acute angle,

 

\[\tan \theta =\left| \frac{2\sqrt{{{h}^{2}}}-ab}{a+b} \right|\]

 

In cosine form

 

\[\cos \theta =\frac{a+b}{\sqrt{{{(a+b)}^{2}}+4{{h}^{2}}}}\]

 

Note:    If two lines are coincident

           

i.e.       \[\theta =0{}^\circ \] or \[180{}^\circ \] 

 

 

then \[\frac{2\sqrt{{{h}^{2}}-ab}}{a+b}=0\]

 

Hence \[{{h}^{2}}=ab\Rightarrow {{h}^{2}}=a\]

 

(b)        If two lines are perpendicular

 

i.e.        \[\theta =90{}^\circ ,\] i.e. \[\tan 90{}^\circ =\infty \]

 

then Loosly, it can be written

 

\[\frac{2\sqrt{{{h}^{2}}-ab}}{a+b}=\infty =\frac{1}{0}\]

 

\[a+b=0\] i.e.

\[\therefore \]Sum of the coefficient of \[{{x}^{2}}\] and \[{{y}^{2}}\] respectively is zero.

 

(c)        The equation of pair of straight lines passing through the origin and perpendicular to the given equation of pair of straight lines\[/a{{x}^{2}}+2hxy+b{{y}^{2}}=0\] is written as \[b{{x}^{2}}-2hxy+a{{x}^{2}}=0\]

The general equation of second degree in x and y be

\[a{{x}^{2}}+b{{y}^{2}}+2hxy+2gx+2fy+c=0\] …….(i)

represents a pair of straight lines iff

\[abc+2fgx-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}=0\]

 

 

(a)        If \[\Delta \ne 0\] & \[{{h}^{2}}-ab\ge 0\] then this general equation of second degree in x & y represents the equation of hyperbola.

(b)        If \[\Delta \ne 0\] & \[{{h}^{2}}-ab\le 0\] then this pair of lines represent the equation ellipse.

(c)        If \[\Delta \ne 0\] & \[{{h}^{2}}-ab=0\]  then this pair of lines represent the equation of parabola

(d)        If \[a=b=1\] & \[h=0\] then this represents the equation of circle.

 

• Some points to remember

 

(a)        Angle between the lines:-

If \[\theta \] is the angle between the two lines:

            \[a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0\]  …… (1)

           

then \[\tan \theta =\pm \left| \frac{2\sqrt{{{h}^{2}}-ab}}{a+b} \right|\]

           

\[\Rightarrow \,\,\,\theta ={{\tan }^{-1}}\left| \frac{2\sqrt{{{h}^{2}}-ab}}{a+b} \right|\]

 

Note:    It is the same form which is obtained by the pair of straight lines passing through the origin.

 

(b)        Point of intersection of lines:

The point of intersection of line (1) is obtained by the partially differentiation of

\[\text{f}\equiv a{{x}^{\text{2}}}+b{{y}^{2}}+2hxy+2gx+2\text{f}y+c=0\]

w.r.t x and y respective & making

           

\[\frac{\partial \text{f}}{\partial x}=0\]                            ….. (i)

           

&  \[\frac{\partial \text{f}}{\partial y}=0\]                        ….. (ii)

Then solve these equations and hence, we will obtain the value ofx and y, which are written as

           

\[(x,y)=\left( \frac{bg-h}{{{h}^{2}}-ab},\frac{a\text{f-gh}}{{{h}^{2}}-ab} \right)\]

Here,

           

\[\frac{\partial \text{f}}{\partial x}=2ax+2hy+2g=0\] & \[\frac{\partial \text{f}}{\partial x}=2by+2hx+2\text{f}=0\]

If the two lines represented by equation (1) be parallel if \[{{h}^{2}}=ab\] & \[b{{g}^{2}}=a{{\text{f}}^{\text{2}}}\]

 

• Distance between the parallel lines: If the two lines represented by (1) are parallel then the distance between these two lines are written as

 

\[d=2\sqrt{\frac{{{g}^{2}}-ac}{a(a+b)}}\]

 

The equation to the pair of lines through the origin and forming an equiletral triangle with line

\[ax+by+c=0\]is given by \[{{(ax+by)}^{2}}-3{{(ay-bx)}^{2}}=0\]

Also, the area of equiletral triangle is

 

\[=\frac{{{c}^{2}}}{\sqrt{3}({{a}^{2}}+{{b}^{2}})}\]

           

The line \[a{{x}^{2}}+b{{y}^{2}}+2hxy=0\] & \[\ell \times +my+n\]

 

= 0 'form issosectes triangle if

 

\[\frac{{{\ell }^{2}}-{{m}^{2}}}{\ell m}=\frac{a-b}{h}\]        

 

Area of the triangle = \[\left| \frac{{{n}^{2}}\sqrt{{{h}^{2}}-ab}}{a{{m}^{2}}-2h\ell m+b{{\ell }^{2}}} \right|\]

 

• Equation of the bisector of the angle between the pair of straight line \[a{{x}^{2}}+2hxy+b{{y}^{2}}=0\] can be written as

 

\[\frac{{{x}^{2}}-{{y}^{2}}}{a-b}=\frac{xy}{h}\]

 

• The equation of the lines joining the origin to the point of intersection of a given line & a given curve.

Let the straight line is

\[y=mx+c\]

 

\[\Rightarrow y-mx=c\Rightarrow \frac{y-mx}{c}=1\]

 

& The equation of the curve is

\[a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2\text{f}y+K=0\]

 

 

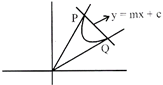
Let the line cuts the curve at point P & Q then the joint equation of OP & OQ be written as

 

\[a{{x}^{2}}+2hxy+b{{y}^{2}}+(2gx+2\text{f}y)+K{{\left( \frac{y-mx}{c} \right)}^{2}}=0\]

 

From this method we can make any pair of equation to be homogenous with the help of the equation of the line.