Answer:
(i) Here, we draw a \[\Delta ABC.\] In which, AB = 3 cm, BC = 3.5 cm and AC = 39 cm Now, by adding two sides of \[\Delta ABC\] i.e. AB + BC = 3 + 3.5 = cm Clearly, AB + B C > AC 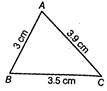 (ii) Here, we draw a \[\Delta ABC\]in which AB = 3 cm, BC = 4 cm and AC = 5 cm Now, by adding two sides of \[\Delta ABC\] i.e. AB + BC = 3 + 4 = 7 cm Clearly, AB + BC > AC
(ii) Here, we draw a \[\Delta ABC\]in which AB = 3 cm, BC = 4 cm and AC = 5 cm Now, by adding two sides of \[\Delta ABC\] i.e. AB + BC = 3 + 4 = 7 cm Clearly, AB + BC > AC 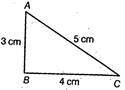 (iii) Here, we draw a \[\Delta ABC\]in which AB = BC = AC = 2.5 cm Now, by adding two sides of \[\Delta ABC\] i.e. AB + BC = 2.5 + 2.5 = 5 cm Clearly, AB + BC > AC
(iii) Here, we draw a \[\Delta ABC\]in which AB = BC = AC = 2.5 cm Now, by adding two sides of \[\Delta ABC\] i.e. AB + BC = 2.5 + 2.5 = 5 cm Clearly, AB + BC > AC 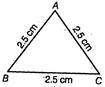 (iv) Here, we draw a \[\Delta ABC\] in which AB = 3 cm, BC = 3.5 cm and AC =4 cm Now, by adding two sides of \[\Delta ABC\] i.e. AB + BC = 3 + 3.5 = 6.5 cm Clearly, AB + BC > AC
(iv) Here, we draw a \[\Delta ABC\] in which AB = 3 cm, BC = 3.5 cm and AC =4 cm Now, by adding two sides of \[\Delta ABC\] i.e. AB + BC = 3 + 3.5 = 6.5 cm Clearly, AB + BC > AC 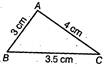 (v) Here, we draw a \[\Delta ABC\] in which AB = 2 cm, BC = 4 cm and AC = 45 cm Now, by adding two sides of \[\Delta ABC\] i.e. AB + BC = 2 + 4 = 6 cm Clearly, AB + BC > AC
(v) Here, we draw a \[\Delta ABC\] in which AB = 2 cm, BC = 4 cm and AC = 45 cm Now, by adding two sides of \[\Delta ABC\] i.e. AB + BC = 2 + 4 = 6 cm Clearly, AB + BC > AC 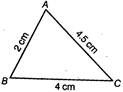 From all these conclusions, we observe that in each case, the sum of the lengths of any two sides is greater than the third 4 cm side. So, the sum of the lengths of any two sides can never be less than the third side.
From all these conclusions, we observe that in each case, the sum of the lengths of any two sides is greater than the third 4 cm side. So, the sum of the lengths of any two sides can never be less than the third side.
You need to login to perform this action.
You will be redirected in
3 sec
