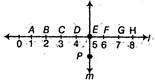
 (a) Is CE = EG? (b) Does PE bisect CG? (c) Identify any two line segments for which PE is the perpendicular bisector. (d) Are these true? (i) AC > FG (ii) CD = GH (vi) BC < EH
(a) Is CE = EG? (b) Does PE bisect CG? (c) Identify any two line segments for which PE is the perpendicular bisector. (d) Are these true? (i) AC > FG (ii) CD = GH (vi) BC < EH
Answer:
(a) From given figure, CE = CD + DE [CD = DE = 1 unit] = 1 + 1 = 2 units and EG = EF + FG [EF = FG = 1 unit] = 1 + 1 = 2 units \[\therefore \] CE = BG = 2 units (b) Since, CE = EG So, E is the mid-point of CG. Thus, PE bisects CG (c) In the given figure, we can see that PE is perpendicular to the given line segment. Since, DE = EF [each = 1 unit] So, PE is the perpendicular bisector of DF. Again, CE = EG [each = 2 units] So, PE is the perpendicular bisector of CG. (d) (i) Here, AC = AB + BC = 1 + 1 = 2units [AB = BC = 1 unit] and FG = 1 unit \[\therefore \] AC > FG is true. (ii) Here, CD = 1 unit and GH = 1 unit CD = GH is true. (iii) Here, BC = 1 unit and EH = EF + FG + GH = 1+ 1 + 1 = 3 units \[\therefore \] BC < EH is true.
You need to login to perform this action.
You will be redirected in
3 sec
